题目内容
| |||||||||||||||
解析:
(1) |
解:
|
(2) |
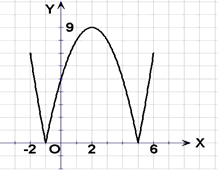
解:方程f(x)=5的解分别是
由于 |
(3) |
解法一:当x∈[-1,5]时,
∵k>2 ∴ ① 当
则g(x)min>0 ② 当 由①、②可知,当k>2时,g(x)>0,x∈[-1,5]. 因此,在区间[-1,5]上, 解法二:当x∈[-1,5]时,f(x)=-x2+4x+5. 由 令△=(k-4)2-4(3k-5)=0,解得k=2或k=18, 在区间[-1,5]上,当k=2时,y=2(x+3)的图像与函数f(x)的图像只交于一点(1,8); 当k=18时,y=18(x+3)的图像与函数f(x)的图像没有交点. 如图可知,由于直线y=k(x+3)过点(-3,0),当k>2时,直线y=k(x+3)是由直线y=2(x+3)绕点(-3,0)逆时针方向旋转得到.因此,在区间[-1,5]上,y=k(x+3)的图像位于函数f(x)图像的上方. |

 名校课堂系列答案
名校课堂系列答案
| |||||||||||