题目内容
8.90×91×92×…×100=( )| A. | A${\;}_{100}^{10}$ | B. | A${\;}_{100}^{11}$ | C. | A${\;}_{100}^{12}$ | D. | A${\;}_{101}^{11}$ |
分析 根据排列数的公式${A}_{n}^{m}$=n(n-1)(n-2)…(n-m+1),写出结果即可.
解答 解:根据排列数的公式,得;
90×91×92×…×100=${A}_{100}^{100-90+1}$=${A}_{100}^{11}$.
故选:B.
点评 本题考查了排列数公式的逆用问题,是基础题目.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
19. 某校对高一年级学生的数学成绩进行统计,全年级同学的成绩全部介于60分与100分之间,将他们的成绩数据绘制成如图所示的频率分布直方图.现从全体学生中,采用分层抽样的方法抽取60名同学的试卷进行分析,则从成绩在[90,100]内的学生中抽取的人数为( )
某校对高一年级学生的数学成绩进行统计,全年级同学的成绩全部介于60分与100分之间,将他们的成绩数据绘制成如图所示的频率分布直方图.现从全体学生中,采用分层抽样的方法抽取60名同学的试卷进行分析,则从成绩在[90,100]内的学生中抽取的人数为( )
 某校对高一年级学生的数学成绩进行统计,全年级同学的成绩全部介于60分与100分之间,将他们的成绩数据绘制成如图所示的频率分布直方图.现从全体学生中,采用分层抽样的方法抽取60名同学的试卷进行分析,则从成绩在[90,100]内的学生中抽取的人数为( )
某校对高一年级学生的数学成绩进行统计,全年级同学的成绩全部介于60分与100分之间,将他们的成绩数据绘制成如图所示的频率分布直方图.现从全体学生中,采用分层抽样的方法抽取60名同学的试卷进行分析,则从成绩在[90,100]内的学生中抽取的人数为( )| A. | 24 | B. | 18 | C. | 15 | D. | 12 |
19.同时投掷两颗骰子,则两颗骰子向上的点数相同的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
16.已知等差数列{an}的前n项和为Sn,若$\overrightarrow{OB}$=a1 $\overrightarrow{OA}$+a2011$\overrightarrow{OC}$,且A、B、C三点共线(O为该直线外一点),则S2011=( )
| A. | 2011 | B. | $\frac{2011}{2}$ | C. | 22011 | D. | 2-2011 |
12.在△ABC中,已知$\overrightarrow{AB}•\overrightarrow{AC}$=2$\sqrt{3}$,A=60°,则△ABC的面积为( )
| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
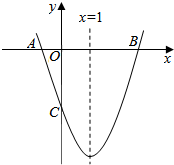 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B. 是
是 上的奇函数,且
上的奇函数,且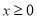 时,
时, ,则
,则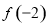 的值为____________.
的值为____________. 如图,已知圆O:x2+y2=4与轴正半轴交于点P,A(-1,0),B(1,0),直线l与圆O切于点S(l不垂直于x轴),抛物线过两点A,B且以l为准线.
如图,已知圆O:x2+y2=4与轴正半轴交于点P,A(-1,0),B(1,0),直线l与圆O切于点S(l不垂直于x轴),抛物线过两点A,B且以l为准线.