题目内容
在数列{an}中,已知 an+1=an-4且 3a4=7a7,Sn为数列{an}的前n项和,Sn有最大值还是最小值?求出这个最值.
解:∵an+1=an-4
∴an+1-an=-4
∴数列{an}为公差为-4数列的等差数列
∵3a4=7a7
∴a1=33
∴an=-4n+37
令an≥0
∴n≤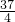
∴等差数列{an}的前9项均为正从第10项开始均为负
∴数列{an}的前n项和Sn有最大值
∴(sn)mnx=s9=9×33- ×9×8×(-4)=153
×9×8×(-4)=153
即数列{an}的前n项和Sn有最大值且最大值为153
分析:根据an+1=an-4可得出数列{an}为等差数列且公差为-4再根据 3a4=7a7即可求出a1从而求出通项an=-4n+37可令an≥0求出n的范围再结合等差数列的函数特性就可判断出等差数列{an}中项的正负的分布情况进而可求出Sn有最大值还是有最小值然后根据等差数列的前n项和公式即可求出这个最值.
点评:本题主要考查了利用等差数列的性质求前n项和的最大最小值.解题的关键是要根据等差数列的函数特性(要么递增要么递减要么是常数列)再结合an≥0求出的n的范围即可对此数列项的正负情况作出判断后问题就迎刃而解了!
∴an+1-an=-4
∴数列{an}为公差为-4数列的等差数列
∵3a4=7a7
∴a1=33
∴an=-4n+37
令an≥0
∴n≤
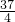
∴等差数列{an}的前9项均为正从第10项开始均为负
∴数列{an}的前n项和Sn有最大值
∴(sn)mnx=s9=9×33-
 ×9×8×(-4)=153
×9×8×(-4)=153即数列{an}的前n项和Sn有最大值且最大值为153
分析:根据an+1=an-4可得出数列{an}为等差数列且公差为-4再根据 3a4=7a7即可求出a1从而求出通项an=-4n+37可令an≥0求出n的范围再结合等差数列的函数特性就可判断出等差数列{an}中项的正负的分布情况进而可求出Sn有最大值还是有最小值然后根据等差数列的前n项和公式即可求出这个最值.
点评:本题主要考查了利用等差数列的性质求前n项和的最大最小值.解题的关键是要根据等差数列的函数特性(要么递增要么递减要么是常数列)再结合an≥0求出的n的范围即可对此数列项的正负情况作出判断后问题就迎刃而解了!

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目