题目内容
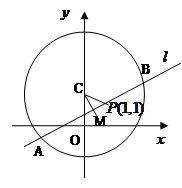
已知圆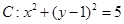 ,直线
,直线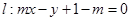 。
。
(Ⅰ)求证:对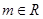 ,直线
,直线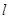 与圆C总有两个不同交点;
与圆C总有两个不同交点;
(Ⅱ)设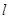 与圆C交与不同两点A、B,求弦AB的中点M的轨迹方程;
与圆C交与不同两点A、B,求弦AB的中点M的轨迹方程;
(Ⅲ)若定点P(1,1)分弦AB为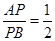 ,求此时直线
,求此时直线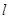 的方程
的方程
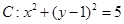 ,直线
,直线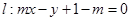 。
。(Ⅰ)求证:对
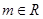 ,直线
,直线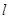 与圆C总有两个不同交点;
与圆C总有两个不同交点;(Ⅱ)设
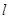 与圆C交与不同两点A、B,求弦AB的中点M的轨迹方程;
与圆C交与不同两点A、B,求弦AB的中点M的轨迹方程;(Ⅲ)若定点P(1,1)分弦AB为
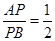 ,求此时直线
,求此时直线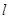 的方程
的方程(Ⅰ)解法一:圆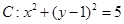 的圆心为
的圆心为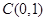 ,半径为
,半径为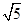 。
。
∴圆心C到直线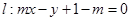 的距离
的距离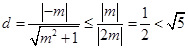
∴直线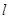 与圆C相交,即直线
与圆C相交,即直线 与圆C总有两个不同交点;
与圆C总有两个不同交点;
方法二:∵直线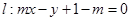 过定点
过定点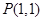 ,而点
,而点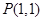 在圆
在圆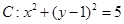 内∴直线
内∴直线 与圆C相交,即直线
与圆C相交,即直线 与圆C总有两个不同交点;
与圆C总有两个不同交点;
(Ⅱ)当M与P不重合时,连结CM、CP,则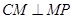 ,
,
∴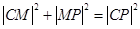
设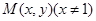 ,则
,则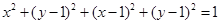 ,
,
化简得: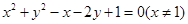
当M与P重合时,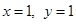 也满足上式。
也满足上式。
故弦AB中点的轨迹方程是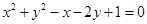 。
。
(Ⅲ)设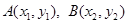 ,由
,由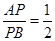 得
得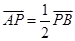 ,
,
∴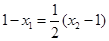 ,化简的
,化简的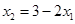 ………………①
………………①
又由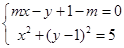 消去
消去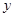 得
得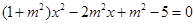 ……………(*)
……………(*)
∴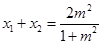 ………………………………②
………………………………②
由①②解得 ,带入(*)式解得
,带入(*)式解得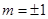 ,
,
∴直线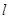 的方程为
的方程为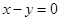 或
或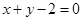
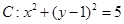 的圆心为
的圆心为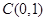 ,半径为
,半径为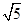 。
。∴圆心C到直线
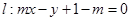 的距离
的距离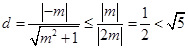
∴直线
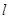 与圆C相交,即直线
与圆C相交,即直线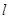 与圆C总有两个不同交点;
与圆C总有两个不同交点;
方法二:∵直线
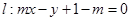 过定点
过定点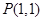 ,而点
,而点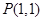 在圆
在圆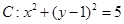 内∴直线
内∴直线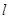 与圆C相交,即直线
与圆C相交,即直线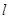 与圆C总有两个不同交点;
与圆C总有两个不同交点;(Ⅱ)当M与P不重合时,连结CM、CP,则
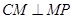 ,
,∴
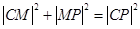
设
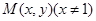 ,则
,则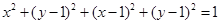 ,
,化简得:
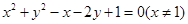
当M与P重合时,
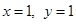 也满足上式。
也满足上式。故弦AB中点的轨迹方程是
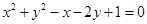 。
。(Ⅲ)设
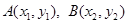 ,由
,由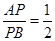 得
得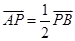 ,
,∴
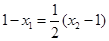 ,化简的
,化简的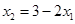 ………………①
………………①又由
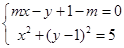 消去
消去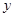 得
得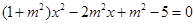 ……………(*)
……………(*)∴
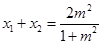 ………………………………②
………………………………②由①②解得
 ,带入(*)式解得
,带入(*)式解得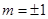 ,
,∴直线
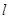 的方程为
的方程为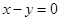 或
或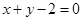
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
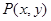 在圆(x-3)2+(y-
在圆(x-3)2+(y-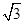 )2=6上运动,则
)2=6上运动,则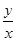 的最大值为__________.
的最大值为__________.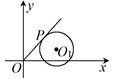
 的切线,切点为A,则切线PA的长为 。
的切线,切点为A,则切线PA的长为 。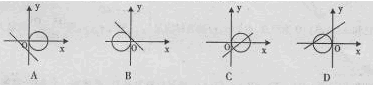
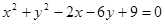 关于直线
关于直线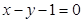 对称的圆的方程为
对称的圆的方程为


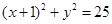 的圆心为C,A(1,0)是圆内一定点,Q为圆周上任意一点,线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程是( )
的圆心为C,A(1,0)是圆内一定点,Q为圆周上任意一点,线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程是( )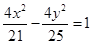
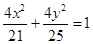
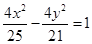
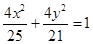
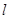 将圆
将圆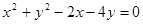 平分,且在两坐标轴上的截距相等,则直线
平分,且在两坐标轴上的截距相等,则直线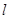 与圆
与圆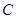 相交于点
相交于点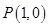 和点
和点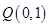 。
。