题目内容
【题目】若函数
在定义域A上的值域为
,则区间A不可能为( )
A.
B.
C.
D.
【答案】D
【解析】
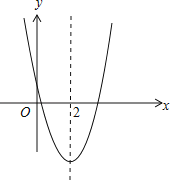
根据函数图象得到函数在R上的单调性是先减后增，再根据单调性分别求出选项中四个区间上的最大最小值，得到相应的值域，再与[﹣3，1]比较，即可得到正确选项．
∵函数f（x）＝x2﹣4x+1的图象是开口向上的抛物线，以x＝2为对称轴，
∴函数在区间（﹣∞，2）上为减函数，[2，+∞）上为增函数．
当x∈[0，4]时，函数最小值为f（2）＝﹣3，最大值为f（0）＝f（4）＝1，得函数值域为[﹣3，1]；
当x∈[2，4]时，函数最小值为f（2）＝﹣3，最大值为f（4）＝1，得函数值域为[﹣3，1]；
当x∈[1，4]时，函数最小值为f（2）＝﹣3，
∵f（1）＝﹣2＜f（4）＝1，∴最大值为f（4）＝1，得函数值域为[﹣3，1]；
当x∈[﹣3，5]时，最小值f（2）＝﹣3，最大值为f（﹣3）＝22，得函数值域为[﹣2，22]．
根据以上的讨论可得区间A不可能为[﹣3，5]．
故选：D．
练习册系列答案
相关题目
