题目内容
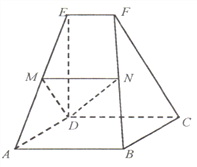
【题目】如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=![]() ,∠BAD=90°.
,∠BAD=90°.
(Ⅰ)求证:AD⊥BC;
(Ⅱ)求异面直线BC与MD所成角的余弦值;
(Ⅲ)求直线CD与平面ABD所成角的正弦值.

【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() ;(Ⅲ)
;(Ⅲ) ![]() .
.
【解析】分析:(Ⅰ)由面面垂直的性质定理可得AD⊥平面ABC,则AD⊥BC.
(Ⅱ)取棱AC的中点N,连接MN,ND.由几何关系可知∠DMN(或其补角)为异面直线BC与MD所成的角.计算可得 .则异面直线BC与MD所成角的余弦值为
.则异面直线BC与MD所成角的余弦值为![]() .
.
(Ⅲ)连接CM.由题意可知CM⊥平面ABD.则∠CDM为直线CD与平面ABD所成的角.计算可得![]() .即直线CD与平面ABD所成角的正弦值为
.即直线CD与平面ABD所成角的正弦值为![]() .
.
详解:(Ⅰ)证明:由平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,AD⊥AB,可得AD⊥平面ABC,故AD⊥BC.
(Ⅱ)取棱AC的中点N,连接MN,ND.又因为M为棱AB的中点,故MN∥BC.所以∠DMN(或其补角)为异面直线BC与MD所成的角.

在Rt△DAM中,AM=1,故DM=![]() .因为AD⊥平面ABC,故AD⊥AC.
.因为AD⊥平面ABC,故AD⊥AC.
在Rt△DAN中,AN=1,故DN=![]() .
.
在等腰三角形DMN中,MN=1,可得 .
.
所以,异面直线BC与MD所成角的余弦值为![]() .
.
(Ⅲ)连接CM.因为△ABC为等边三角形,M为边AB的中点,故CM⊥AB,CM=![]() .又因为平面ABC⊥平面ABD,而CM
.又因为平面ABC⊥平面ABD,而CM![]() 平面ABC,故CM⊥平面ABD.所以,∠CDM为直线CD与平面ABD所成的角.
平面ABC,故CM⊥平面ABD.所以,∠CDM为直线CD与平面ABD所成的角.
在Rt△CAD中,CD=![]() =4.
=4.
在Rt△CMD中, ![]() .
.
所以,直线CD与平面ABD所成角的正弦值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】随着雾霾的日益严重,中国部分省份已经实施了“煤改气”的计划来改善空气质量指数.2017年支撑我国天然气市场消费增长的主要资源是国产常规气和进口天然气,资源每年的增量不足以支撑天然气市场连续![]() 亿立方米的年增量.进口LNG和进口管道气受到接收站、管道能力和进口气价资源的制约.未来,国产常规气产能释放的红利将会逐步减弱,产量增量将维持在
亿立方米的年增量.进口LNG和进口管道气受到接收站、管道能力和进口气价资源的制约.未来,国产常规气产能释放的红利将会逐步减弱,产量增量将维持在![]() 亿方以内.为了测定某市是否符合实施煤改气计划的标准,某监测站点于2016年8月某日起连续
亿方以内.为了测定某市是否符合实施煤改气计划的标准,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数(AQI),数据统计如下:
天监测空气质量指数(AQI),数据统计如下:
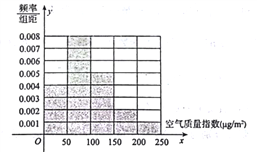
(1)根据上图完成下列表格
空气质量指数( |
|
|
|
|
|
天数 |
(2)计算这![]() 天中,该市空气质量指数的平均数;
天中,该市空气质量指数的平均数;
(3)若按照分层抽样的方法,从空气质量指数在![]() 以及
以及![]() 的等级中抽取
的等级中抽取![]() 天进行调研,再从这
天进行调研,再从这![]() 天中任取
天中任取![]() 天进行空气颗粒物分析,求恰有
天进行空气颗粒物分析,求恰有![]() 天空气质量指数在
天空气质量指数在![]() 上的概率.
上的概率.