题目内容
设函数f(x)=(x2+2)lnx,g(x)=2x2+ax,a∈R
(1)证明:f(x)是(0,+∞)上的增函数;
(2)设F(x)=f(x)-g(x),当x∈[1,+∞)时,F(x)≥0恒成立,求a的取值范围.
(1)证明:f(x)是(0,+∞)上的增函数;
(2)设F(x)=f(x)-g(x),当x∈[1,+∞)时,F(x)≥0恒成立,求a的取值范围.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)证明f'(x)≥0在(0,+∞)恒成立,通过构造h(x)=2lnx+
+1,x∈(0,+∞),求出函数的导数两条函数的最小值大于0,即可证明f(x)是(0,+∞)上的增函数.------(6分)
(2)化简F(x)=f(x)-g(x)=(x2+2)lnx-2x2-ax≥0,转化为:a在一侧的不等式,构造函数G(x)=
.通过导数判断函数的单调性求出最小值,即可求解a的范围.
| 2 |
| x2 |
(2)化简F(x)=f(x)-g(x)=(x2+2)lnx-2x2-ax≥0,转化为:a在一侧的不等式,构造函数G(x)=
| (x2+2)lnx-2x2 |
| x |
解答:
解:(1)若证明f(x)是(0,+∞)上的增函数,只需证明f'(x)≥0在(0,+∞)恒成立,
即:f′(x)=2xlnx+
+x≥0?x(2lnx+
+1)≥0?2lnx+
+1≥0-------(4分)
设h(x)=2lnx+
+1,x∈(0,+∞),h′(x)=
-
=
所以:h(x)在(0,
)上递减,(
,+∞)上递增,h(x)最小值h(
)=ln2+2>0
故:f′(x)=2xlnx+
+x=xh(x)>0,所以:f(x)是(0,+∞)上的增函数.------(6分)
(2)由F(x)=f(x)-g(x)=(x2+2)lnx-2x2-ax≥0得:
a≤
在x∈[1,+∞)上恒成立,------------(8分)
设G(x)=
则G′(x)=
,
所以g(x)在(1,
)递增,(
,e)递减,(e,+∞)递增------------(9分)
所以G(x)的最小值为G(1),G(e)中较小的,G(e)-G(1)=
-e+2>0,
所以:G(e)>G(1),即:G(x)在x∈[1,+∞)的最小值为G(1)=-2,--------(11分)
只需a≤-2-------(12分)
即:f′(x)=2xlnx+
| 2 |
| x |
| 2 |
| x2 |
| 2 |
| x2 |
设h(x)=2lnx+
| 2 |
| x2 |
| 2 |
| x |
| 4 |
| x3 |
| 2x2-4 |
| x3 |
所以:h(x)在(0,
| 2 |
| 2 |
| 2 |
故:f′(x)=2xlnx+
| 2 |
| x |
(2)由F(x)=f(x)-g(x)=(x2+2)lnx-2x2-ax≥0得:
a≤
| (x2+2)lnx-2x2 |
| x |
设G(x)=
| (x2+2)lnx-2x2 |
| x |
则G′(x)=
| (x2-2)(lnx-1) |
| x2 |
所以g(x)在(1,
| 2 |
| 2 |
所以G(x)的最小值为G(1),G(e)中较小的,G(e)-G(1)=
| 2 |
| e |
所以:G(e)>G(1),即:G(x)在x∈[1,+∞)的最小值为G(1)=-2,--------(11分)
只需a≤-2-------(12分)
点评:本题考查函数的导数的综合应用,构造法求解函数的最值的应用,考查分析问题与解决问题的能力,难度比较大,考查转化思想的应用.

练习册系列答案
相关题目
不等式|x|(2x-1)≤0的解集是( )
A、(-∞,
| ||
B、(-∞,0)∪(0,
| ||
C、[-
| ||
D、[0,
|
过抛物线y2=4x的焦点F作两条互相垂直的直线l1,l2,l1交C于A、B,l2交C于M、N.则
+
=( )
| 1 |
| |AB| |
| 1 |
| |MN| |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
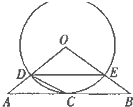 如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.
如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB. 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则球的表面积是
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则球的表面积是