题目内容
已知命题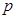 :函数
:函数 在
在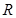 上单调递增;命题
上单调递增;命题 :不等式
:不等式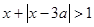 的解集为
的解集为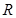 ,若
,若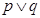 为真,
为真,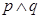 为假,求实数
为假,求实数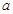 的取值范围.
的取值范围.
【答案】
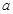 的取值范围是
的取值范围是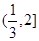 .
.
【解析】
试题分析:若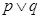 为真,则
为真,则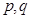 中至少有一个为真,
中至少有一个为真,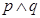 为假,则
为假,则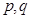 中至少有一个为假,由此可得
中至少有一个为假,由此可得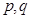 中一真一假,故有
中一真一假,故有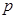 真
真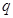 假,与
假,与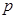 假
假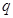 真两种情况,因此当
真两种情况,因此当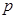 真时求出
真时求出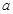 的取值范围,当
的取值范围,当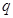 真时求出
真时求出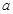 的取值范围,求出这两种情况的并集与交集,并集中除去交集部分即为所求.
的取值范围,求出这两种情况的并集与交集,并集中除去交集部分即为所求.
试题解析:若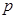 真,则
真,则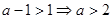 2分
2分
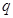 真
真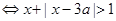 恒成立,设
恒成立,设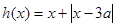 ,则
,则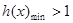
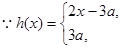
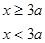 ,易知
,易知
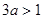 ,即
,即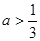 6分
6分
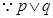 为真,
为真,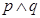 为假
为假 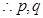 一真一假
7分
一真一假
7分
(1)若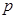 真
真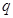 假,则
假,则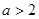 且
且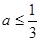 ,矛盾
9分
,矛盾
9分
(2)若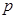 假
假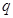 真,则
真,则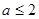 且
且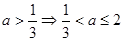 ,
11分
,
11分
综上可知,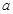 的取值范围是
的取值范围是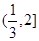 12分
12分
考点:简易逻辑,指数函数,绝对值不等式的解法.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
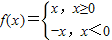 为偶函数;
为偶函数;