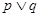题目内容
已知命题:①函数
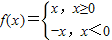 为偶函数;
为偶函数;②定义在R上的函数f(x)在区间(-∞,0]上是单调减函数,在区间(0,+∞)上也是单调减函数,则函数f(x)在R上是单调减函数;
③函数f(x)=loga(x-1)+3的图象一定过定点;
④函数y=|3-x2|的图象和函数y=a的图象的公共点个数为m,则m的值不可能是1.
其中正确命题的序号为 .
【答案】分析:分别利用奇偶函数的定义域,函数的单调性和基本初等函数的性质分别判断.
解答: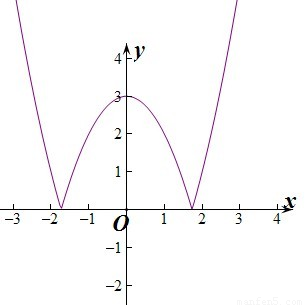 解:①因为函数f(x)的图象关于y轴对称,所以函数f(x)是偶函数,所以①正确.
解:①因为函数f(x)的图象关于y轴对称,所以函数f(x)是偶函数,所以①正确.
②若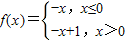 满足条件,但函数在R上不单调,所以②错误.
满足条件,但函数在R上不单调,所以②错误.
③当x=2时,f(2)=loga(2-1)+3=3,所以函数f(x)=loga(x-1)+3的图象一定过定点(2,3),所以③正确.
④作出函数y=|3-x2|的图象如图:
由图象可知函数为偶函数,所以函数y=|3-x2|的图象和函数y=a的图象的公共点个数为0个或4个或3个或2个,所以则m的值不可能是1个,所以④正确.
故答案为:①③④.
点评:本题主要考查函数的图象和性质的应用,要求熟练掌握函数的基本性质.
解答:
 解:①因为函数f(x)的图象关于y轴对称,所以函数f(x)是偶函数,所以①正确.
解:①因为函数f(x)的图象关于y轴对称,所以函数f(x)是偶函数,所以①正确.②若
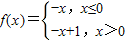 满足条件,但函数在R上不单调,所以②错误.
满足条件,但函数在R上不单调,所以②错误.③当x=2时,f(2)=loga(2-1)+3=3,所以函数f(x)=loga(x-1)+3的图象一定过定点(2,3),所以③正确.
④作出函数y=|3-x2|的图象如图:
由图象可知函数为偶函数,所以函数y=|3-x2|的图象和函数y=a的图象的公共点个数为0个或4个或3个或2个,所以则m的值不可能是1个,所以④正确.
故答案为:①③④.
点评:本题主要考查函数的图象和性质的应用,要求熟练掌握函数的基本性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
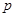 :抛物线
:抛物线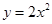 的准线方程为
的准线方程为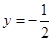 ;命题
;命题 :若函数
:若函数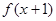 为偶
为偶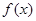 关于
关于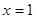 对称.则下列命题是真命题的是
对称.则下列命题是真命题的是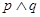 B.
B.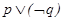 C.
C.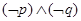 D.
D.