题目内容
已知集合A={（x，y）|y=|x-1|，x，y∈R}，B={（x，y）|y=ax+2，x，y∈R}，若集合A∩B有且只有一个元素，则实数a的取值范围是分析：由条件“集合A∩B有且只有一个元素”可联立方程组转化成方程只有一解，再转化成两个函数图象只有一个交点，结合图象即可得到实数a的取值范围．
解答：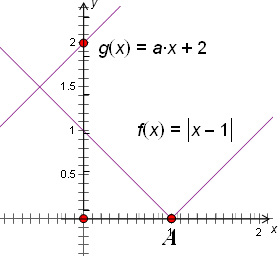
解：∵集合A与集合B都是点集，集合A∩B有且只有一个元素
∴方程组
有且只有一个解
结合函数的图象
可知：实数a的取值范围是 （-∞，-1]∪[1，+∞），
故答案为（-∞，-1]∪[1，+∞）
解：∵集合A与集合B都是点集，集合A∩B有且只有一个元素∴方程组
|
结合函数的图象
可知：实数a的取值范围是 （-∞，-1]∪[1，+∞），
故答案为（-∞，-1]∪[1，+∞）
点评：本题主要考查了集合的包含关系判断及其应用，属于考查对课本中概念的理解，属于基础题．
练习册系列答案
相关题目