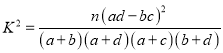题目内容
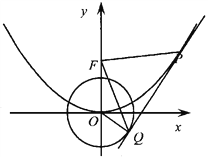
【题目】如图,O为坐标原点,点F为抛物线C1: ![]() 的焦点,且抛物线C1上点M处的切线与圆C2:
的焦点,且抛物线C1上点M处的切线与圆C2: ![]() 相切于点Q.
相切于点Q.
![]()
![]()
(Ⅰ)当直线MQ的方程为![]() 时,求抛物线C1的方程;
时,求抛物线C1的方程;
(Ⅱ)当正数p变化时,记S1 ,S2分别为△FMQ,△FOQ的面积,求![]() 的最小值.
的最小值.
【答案】(1)x2![]() y(2)
y(2)![]()
【解析】试题分析:(1)依据题设条件,借助导数的几何意义求出切点坐标及其斜率![]() ,建立方程组求解;(2)运用直线与圆相切的建立等量关系
,建立方程组求解;(2)运用直线与圆相切的建立等量关系![]() ,通过解方程组求得点Q的坐标,进而求出S1 ,S2,建立目标函数
,通过解方程组求得点Q的坐标,进而求出S1 ,S2,建立目标函数![]() ,然后运用基本不等式求解:
,然后运用基本不等式求解:
解:(Ⅰ)设点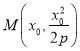 ,由
,由![]() 得,
得, ![]() ,求导
,求导![]() ,
,
而直线![]() 的斜率为1,所以
的斜率为1,所以![]() 且
且![]() ,解得
,解得![]()
所以抛物线标准方程为![]()
(Ⅱ)因为点M处的切线方程为: ![]() ,即
,即![]() ,
,
根据切线又与圆相切,得![]() ,即
,即 ,化简得
,化简得![]() ,
,
由方程组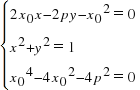 ,解得Q(
,解得Q(![]() ,
,![]() ),
),
所以|PQ|=![]() |xP-xQ|=
|xP-xQ|=![]()
![]() =
=![]() ,
,
点F(0,![]() )到切线PQ的距离是d=
)到切线PQ的距离是d=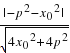 =
=![]()
![]() ,
,
所以![]() =
=![]() ×
×![]()
![]() ×
×![]()
![]() =
=![]() ,
,
![]() =
=![]() ,
,
而由![]() 知,4p2=
知,4p2=![]() ,得|x0|>2,
,得|x0|>2,
所以![]() =
=![]() =
=![]() =
=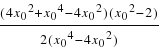
=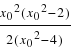 =
=![]() +3≥2
+3≥2![]() +3,当且仅当
+3,当且仅当![]() 时取“=”号,即
时取“=”号,即![]() ,此时,p=
,此时,p=![]() ,所以
,所以![]() 的最小值为
的最小值为![]() .
.
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案【题目】国家“十三五”计划,提出创新兴国,实现中国创新,某市教育局为了提高学生的创新能力,把行动落到实处,举办一次物理、化学综合创新技能大赛,某校对其甲、乙、丙、丁四位学生的物理成绩(x)和化学成绩(y)进行回归分析,求得回归直线方程为y=1.5x﹣35.由于某种原因,成绩表(如表所示)中缺失了乙的物理和化学成绩.
甲 | 乙 | 丙 | 丁 | |
物理成绩(x) | 75 | m | 80 | 85 |
化学成绩(y) | 80 | n | 85 | 95 |
综合素质 | 155 | 160 | 165 | 180 |
(1)请设法还原乙的物理成绩m和化学成绩n;
(2)在全市物理化学科技创新比赛中,由甲、乙、丙、丁四位学生组成学校代表队参赛.共举行3场比赛,每场比赛均由赛事主办方从学校代表中随机抽两人参赛,每场比赛所抽的选手中,只要有一名选手的综合素质分高于160分,就能为所在学校赢得一枚荣誉奖章.若记比赛中赢得荣誉奖章的枚数为ξ,试根据上表所提供数据,预测该校所获奖章数ξ的分布列与数学期望.
【题目】近代统计学的发展起源于二十世纪初,它是在概率论的基础上发展起来的,统计性质的工作可以追溯到远古的“结绳记事”和《二十四史》中大量的关于我人口、钱粮、 水文、天文、地震等资料的记录.近几年,雾霾来袭,对某市该年11月份的天气情况进行统计,结果如下:表一
日期 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
天气 | 晴 | 霾 | 霾 | 阴 | 霾 | 霾 | 阴 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 霾 |
日期 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
天气 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 晴 | 霾 | 晴 | 霾 | 霾 | 霾 | 晴 | 霾 |
由于此种情况某市政府为减少雾霾于次年采取了全年限行的政策.
下表是一个调査机构对比以上两年11月份(该年不限行![]() 天、次年限行
天、次年限行![]() 天共
天共![]() 天)的调查结果:
天)的调查结果:
表二
不限行 | 限行 | 总计 | |
没有雾霾 |
| ||
有雾霾 |
| ||
总计 |
|
|
|
(1)请由表一数据求![]() ,并求在该年11月份任取一天,估计该市是晴天的概率;
,并求在该年11月份任取一天,估计该市是晴天的概率;
(2)请用统计学原理计算若没有![]() 的把握认为雾霾与限行有关系,则限行时有多少天没有雾霾?
的把握认为雾霾与限行有关系,则限行时有多少天没有雾霾?
(由于不能使用计算器,所以表中数据使用时四舍五入取整数)
|
|
|
|
|
|
|
|
|
|