题目内容
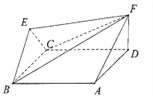
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
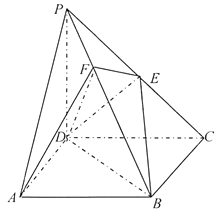
如图,在阳马![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 为
为![]() 中点,点
中点,点![]() 在
在![]() 上,且
上,且![]() 平面
平面![]() ,连接
,连接![]() ,
, ![]() .
.
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)试判断四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(Ⅲ)已知![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)![]() .
.
【解析】试题分析:
(1)利用线面垂直的判断定理证明![]() 垂直于平面
垂直于平面![]() 内的两条相交直线即可;
内的两条相交直线即可;
(2)利用空间几何体的结构特征判断命题是否成立即可;
(3)利用题意建立空间直角坐标系,求得法向量,最后利用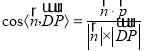 求解角度值即可求得余弦值.
求解角度值即可求得余弦值.
试题解析:
(Ⅰ)因为![]() 面
面![]() ,
, ![]() 面
面![]() ,所以
,所以![]() .
.
因为四边形![]() 为矩形,所以
为矩形,所以![]() .
.
![]() ,所以
,所以![]() 面
面![]() .
.
![]() 面
面![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() 为
为![]() 中点,所以
中点,所以![]() .
.
![]() ,
,
所以![]() 面
面![]() .
.
(Ⅱ)四面体![]() 是鳖臑,其中
是鳖臑,其中![]() ,
, ![]() .
.
(Ⅲ)以![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
设![]() ,则
,则![]() .
.
![]() 得
得![]() 解得
解得![]() .所以
.所以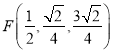 .
.
设平面![]() 的法向量
的法向量![]() ,
,
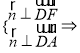
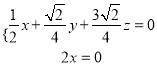 令
令![]() 得
得![]() ,
, ![]() .
.
平面![]() 的法向量
的法向量![]() ,
,
平面![]() 的法向量
的法向量![]() ,
,
![]() ,
, 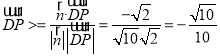 .
.
二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】学校为了了解高三学生每天自主学习中国古典文学的时间,随机抽取了高三男生和女生各50名进行问卷调查,其中每天自主学习中国古典文学的时间超过3小时的学生称为“古文迷”,否则为“非古文迷”,调查结果如表:
古文迷 | 非古文迷 | 合计 | |
男生 | 26 | 24 | 50 |
女生 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据表中数据判断能否有![]() 的把握认为“古文迷”与性别有关?
的把握认为“古文迷”与性别有关?
(2)先从调查的女生中按分层抽样的方法抽出5人进行理科学习时间的调查,求所抽取的5人中“古文迷”和“非古文迷”的人数;
(3)现从(2)中所抽取的5人中再随机抽取3人进行体育锻炼时间的调查,记这3人中“古文迷”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
参考公式: 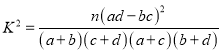 ,其中
,其中![]() .
.