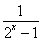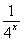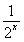题目内容
设a>0,f(x)=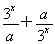 是R上的偶函数.
是R上的偶函数.
(1)求a的值;
(2)判断并证明函数f(x)在[0,+∞)上的单调性;
(3)求函数的值域.
(1)a=1(2)f(x)在[0,+∞)上为增函数(3)[2,+∞)
【解析】(1)因为f(x)为偶函数,故f(1)=f(-1),
于是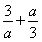 =
=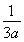 +3a,即
+3a,即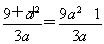 .因为a>0,故a=1.
.因为a>0,故a=1.
(2)设x2>x1≥0,f(x1)-f(x2)=(3x2-3x1)(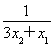 -1).
-1).
因为3x为增函数,且x2>x1,
故3x2-3x1>0.因为x2>0,x1≥0,故x2+x1>0,于是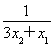 <1,即
<1,即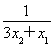 -1<0,所以f(x1)-f(x2)<0,所以f(x)在[0,+∞)上为增函数.
-1<0,所以f(x1)-f(x2)<0,所以f(x)在[0,+∞)上为增函数.
(3)因为函数为偶函数,且f(x)在[0,+∞)上为增函数,故f(0)=2为函数的最小值,于是函数的值域为[2,+∞).

练习册系列答案
相关题目