题目内容
点A为两曲线C1: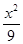 +
+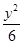 =1和C2:x2-
=1和C2:x2-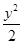 =1在第二象限的交点,B、C为曲线C1的左、右焦点,线段BC上一点P满足:
=1在第二象限的交点,B、C为曲线C1的左、右焦点,线段BC上一点P满足: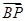 =
=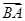 +m(
+m(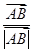 +
+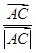 ),则实数m的值为 .
),则实数m的值为 .
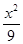 +
+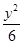 =1和C2:x2-
=1和C2:x2-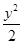 =1在第二象限的交点,B、C为曲线C1的左、右焦点,线段BC上一点P满足:
=1在第二象限的交点,B、C为曲线C1的左、右焦点,线段BC上一点P满足: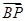 =
=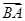 +m(
+m(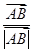 +
+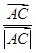 ),则实数m的值为 .
),则实数m的值为 .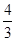
法一 ∵A是曲线C1与C2在第二象限的交点如图所示.
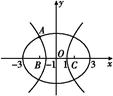
∴由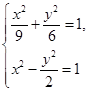
得点A坐标为(-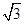 ,2).
,2).
由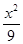 +
+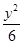 =1知c2=9-6=3,
=1知c2=9-6=3,
∴B(-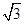 ,0),C(
,0),C(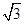 ,0),
,0),
∴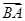 =(0,2),
=(0,2),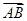 =(0,-2),
=(0,-2),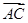 =(2
=(2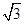 ,-2).
,-2).
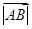 =2,
=2,
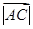 =4.
=4.
∴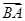 +m(
+m(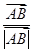 +
+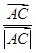 )=(0,2)+m
)=(0,2)+m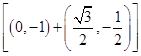 =(0,2)+m(
=(0,2)+m(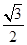 ,-
,-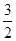 )=(
)=(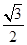 m,2-
m,2-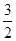 m).
m).
设点P(x,0),则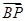 =(x+
=(x+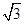 ,0),
,0),
由题意得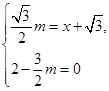
解得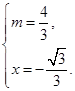
法二 由椭圆与双曲线方程可知,C1、C2有共同的焦点,即B、C.
由椭圆和双曲线定义有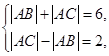
解得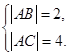
又|BC|=2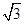 ,
,
∴△ABC为直角三角形,且∠BAC=60°.
又由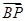 =
=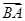 +m(
+m(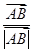 +
+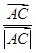 )得
)得
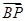 -
-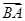 =
=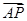 =m(
=m(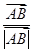 +
+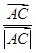 )(*)
)(*)
由向量的线性运算易知,AP为∠BAC的平分线,
故cos∠BAP=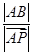 ,
,
即cos 30°=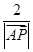 ,
,
∴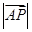 =
=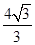 .
.
将(*)式的两边平方得:
|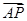 |2=m2(1+1+2cos 60°)=(
|2=m2(1+1+2cos 60°)=(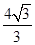 )2,
)2,
解得m=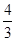 或m=-
或m=-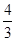 (舍去).
(舍去).

∴由
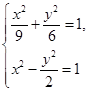
得点A坐标为(-
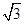 ,2).
,2).由
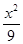 +
+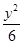 =1知c2=9-6=3,
=1知c2=9-6=3,∴B(-
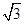 ,0),C(
,0),C(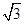 ,0),
,0),∴
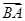 =(0,2),
=(0,2),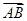 =(0,-2),
=(0,-2),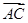 =(2
=(2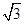 ,-2).
,-2).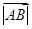 =2,
=2,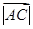 =4.
=4.∴
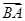 +m(
+m(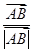 +
+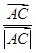 )=(0,2)+m
)=(0,2)+m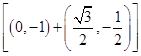 =(0,2)+m(
=(0,2)+m(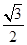 ,-
,-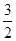 )=(
)=(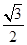 m,2-
m,2-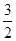 m).
m).设点P(x,0),则
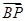 =(x+
=(x+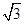 ,0),
,0),由题意得
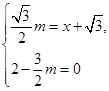
解得
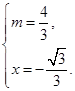
法二 由椭圆与双曲线方程可知,C1、C2有共同的焦点,即B、C.
由椭圆和双曲线定义有
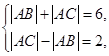
解得
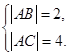
又|BC|=2
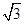 ,
,∴△ABC为直角三角形,且∠BAC=60°.
又由
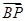 =
=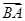 +m(
+m(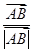 +
+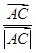 )得
)得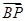 -
-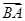 =
=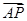 =m(
=m(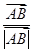 +
+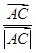 )(*)
)(*)由向量的线性运算易知,AP为∠BAC的平分线,
故cos∠BAP=
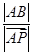 ,
,即cos 30°=
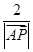 ,
,∴
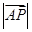 =
=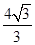 .
.将(*)式的两边平方得:
|
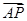 |2=m2(1+1+2cos 60°)=(
|2=m2(1+1+2cos 60°)=(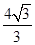 )2,
)2,解得m=
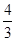 或m=-
或m=-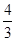 (舍去).
(舍去).
练习册系列答案
相关题目
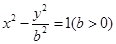 的一条渐近线的方程为
的一条渐近线的方程为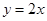 ,则
,则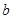 =_____ __.
=_____ __.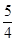 ,则双曲线的标准方程为______________________.
,则双曲线的标准方程为______________________.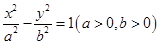 的离心率为2,
的离心率为2,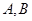 为期左右顶点,点P为双曲线C在第一象限的任意一点,点O为坐标原点,若
为期左右顶点,点P为双曲线C在第一象限的任意一点,点O为坐标原点,若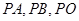 的斜率为
的斜率为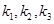 ,则
,则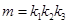 的取值范围为( )
的取值范围为( )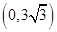
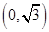
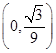
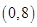
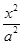 -
-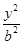 =1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的渐近线方程为( )
=1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的渐近线方程为( )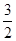 x
x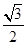 x
x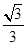 x
x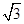 x
x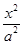 -
-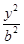 =1(a>0,b>0)的一条渐近线方程是y=
=1(a>0,b>0)的一条渐近线方程是y=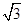 x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )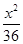 -
-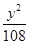 =1
=1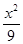 -
-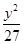 =1
=1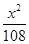 -
-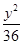 =1
=1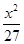 -
-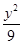 =1
=1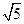 ,0),点P在双曲线上,且线段PF1的中点坐标为(0,2),则此双曲线的方程是( )
,0),点P在双曲线上,且线段PF1的中点坐标为(0,2),则此双曲线的方程是( )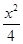 -y2=1
-y2=1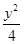 =1
=1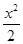 -
-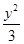 =1
=1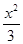 -
-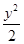 =1
=1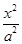 -
-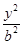 =1的离心率为2,焦点与椭圆
=1的离心率为2,焦点与椭圆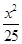 +
+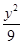 =1的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为 .
=1的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为 .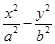 =1(a>0,b>0)与双曲线C2:
=1(a>0,b>0)与双曲线C2: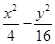 =1有相同的渐近线,且C1的右焦点为F(
=1有相同的渐近线,且C1的右焦点为F(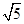 ,0),则a=________,b=________.
,0),则a=________,b=________.