Question

△ABC中，a，b，c分别为∠A，∠B，∠C的对边，如果a，b，c成等差数列，∠B=30°，△ABC的面积为，那么b=________．

Answer 1

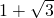
分析：根据等差中项的性质可知2b=a+c．平方后整理得a²+c²=4b²-2ac．利用三角形面积求得ac的值，进而把a²+c²=4b²-2ac．代入余弦定理求得b的值．
解答：∵a，b，c成等差数列，
∴2b=a+c．
平方得a²+c²=4b²-2ac．
又△ABC的面积为，且∠B=30°，
故由S_△=acsinB=ac•sin30°=ac=，
得ac=6，
∴a²+c²=4b²-12．
由余弦定理
cosB====．
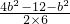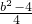解得b²=4+2．
又∵b为边长，
∴b=1+．
故答案为：1+
点评：本题主要考查了解三角形的问题．解题过程中常需要正弦定理，余弦定理，三角形面积公式以及勾股定理等知识．