题目内容
若直线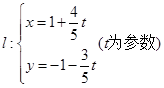 被曲线
被曲线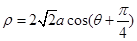 所截得的弦长大于
所截得的弦长大于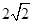 ,求正整数
,求正整数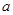 的最小值。
的最小值。
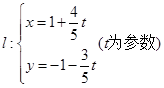 被曲线
被曲线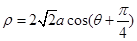 所截得的弦长大于
所截得的弦长大于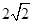 ,求正整数
,求正整数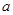 的最小值。
的最小值。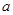 的最小值为2
的最小值为2试题分析:解:把
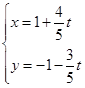 化为普通方程为:
化为普通方程为: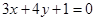 …………2分
…………2分把
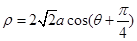 直角坐标系方程为:
直角坐标系方程为: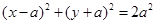 …4分
…4分因为
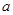 为正整数,所以圆心到直线的距离为
为正整数,所以圆心到直线的距离为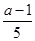 …………7分
…………7分又因为弦长大于
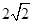 ,所以
,所以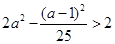 ,解得:
,解得: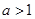 ,所以正整数
,所以正整数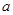 的最小值为2 。 …………10分。
的最小值为2 。 …………10分。点评:解决该试题的关键是能将极坐标方程化为普通方程,以及直线的参数方程化为普通方程,结合圆心到直线的距离来求解最值,属于基础题。

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 有相同的长度单位,以原点
有相同的长度单位,以原点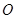 为极点,以
为极点,以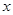 轴正半轴为极轴.已知直线
轴正半轴为极轴.已知直线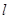 的参数方程为
的参数方程为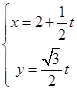 (
(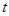 为参数),曲线
为参数),曲线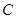 的极坐标方程为
的极坐标方程为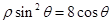 .
.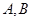 两点,求弦长
两点,求弦长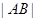 .
.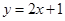 的参数方程是( )。
的参数方程是( )。 (t为参数)
(t为参数)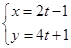 (t为参数)
(t为参数)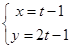 (t为参数)
(t为参数)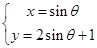 (t为参数)
(t为参数) 和参数方程
和参数方程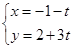 (
(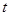 为参数)所表示的图形分别是( )
为参数)所表示的图形分别是( )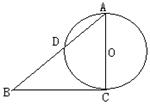
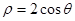 与直线
与直线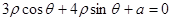 相切,求实数a的值______.
相切,求实数a的值______.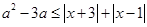 对任意实数
对任意实数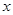 恒成立,求实数
恒成立,求实数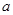 的取值范围____.
的取值范围____.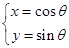 (
( 为参数,
为参数,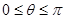 )上的点,点A的坐标为(1,0),
)上的点,点A的坐标为(1,0),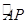 的长度均为
的长度均为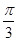 。
。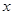 轴的正半轴为极轴建立极坐标系,求点M的极坐标;
轴的正半轴为极轴建立极坐标系,求点M的极坐标;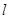 的参数方程为
的参数方程为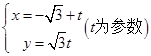 .以原点
.以原点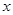 为极点,以
为极点,以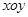 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线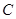 的极坐标方程为
的极坐标方程为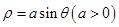 .当直线
.当直线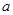 = ;
= ;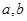 是方程x
是方程x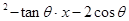 =0的两个实根,那么过点
=0的两个实根,那么过点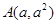 和
和 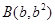 (
( )的直线与曲线
)的直线与曲线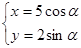 (
(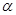 为参数)的位置关系是
为参数)的位置关系是 在直角坐标系
在直角坐标系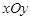 中, 过点
中, 过点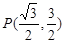 作倾斜角为
作倾斜角为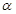 的直线
的直线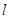 与曲线
与曲线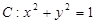 相交于不同的两点
相交于不同的两点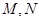 .
.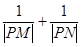 的取值范围.
的取值范围.