题目内容
(本小题满分14分)
如图中,是一个长方体截去一个角所得多面体的直观图.它的正视图和侧视图在右面画出(单位:cm).
(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;
(3)在所给直观图中连接BC′,证明:BC′∥面EFG.

如图中,是一个长方体截去一个角所得多面体的直观图.它的正视图和侧视图在右面画出(单位:cm).
(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;
(3)在所给直观图中连接BC′,证明:BC′∥面EFG.

(1)解:俯视图如图58.
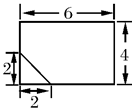 图58 ………4分
图58 ………4分
(2)解:所求多面体体积
V=V长方体-V正三棱锥=4×4×6-××2=(cm3) ………8分
(3)证明:如图59,在长方体ABCD-A′B′C′D′中,
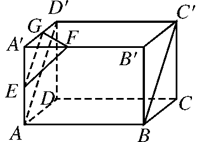
图59
连接AD′,则AD′∥BC′.
因为E、G分别为AA′、A′D′中点,
所以AD′∥EG, ………12分
从而EG∥BC′.又BC′?平面EFG,
所以BC′∥面EFG. ………14分
 图58 ………4分
图58 ………4分(2)解:所求多面体体积
V=V长方体-V正三棱锥=4×4×6-××2=(cm3) ………8分
(3)证明:如图59,在长方体ABCD-A′B′C′D′中,

图59
连接AD′,则AD′∥BC′.
因为E、G分别为AA′、A′D′中点,
所以AD′∥EG, ………12分
从而EG∥BC′.又BC′?平面EFG,
所以BC′∥面EFG. ………14分
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 )如图所示,则此几何体的体积是
)如图所示,则此几何体的体积是  .
.

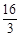
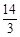
 ,底面积为
,底面积为 ,则该圆锥的体积为_____。
,则该圆锥的体积为_____。 是圆柱的母线,
是圆柱的母线, 是圆柱底面圆的直径,
是圆柱底面圆的直径, 是底面圆周上异于
是底面圆周上异于 的任意一点,
的任意一点, .(Ⅰ)求证:
.(Ⅰ)求证: 平面
平面 ;(Ⅱ)求三棱锥
;(Ⅱ)求三棱锥 的体积的最大值.
的体积的最大值.








 、
、 、
、 ,这个长方体对角线的长是 [ ]
,这个长方体对角线的长是 [ ]