题目内容
正三棱锥P-ABC高为2,侧棱与底面所成角为45°,则点 A到侧面PBC的距离是

分析:在立体几何中,求点到平面的距离是一个常见的题型,同时求直线到平面的距离、平行平面间的距离及多面体的体积也常转化为求点到平面的距离.本题采用的是“找垂面法”:即找(作)出一个过该点的平面与已知平面垂直,然后过该点作其交线的垂线,则得点到平面的垂线段.设P在底面ABC上的射影为O,则PO=2,且O是三角形ABC的中心,设底面边长为a,
 ?
?  a=2∴a="2"
a=2∴a="2"  设侧棱为b,则b="2"
设侧棱为b,则b="2"  斜高h′=
斜高h′=  .由面积法求A到侧面PBC的距离h=
.由面积法求A到侧面PBC的距离h=  =
=  .
.解:如图所示:设P在底面ABC上的射影为O,
则PO⊥平面ABC,PO=2,且O是三角形ABC的中心,
∴BC⊥AM,BC⊥PO,PO∩AM=0
∴BC⊥平面APM
又∵BC?平面ABC,
∴平面ABC⊥平面APM,
又∵平面ABC∩平面APM=PM,
∴A到侧面PBC的距离即为△APM的高
设底面边长为a,
则
 ?
?  a=2∴a="2"
a=2∴a="2" 
设侧棱为b,则b=2
 斜高h′=
斜高h′= .
.由面积法求A到侧面PBC的距离h=
 =
=
故答案为:


点评:本小题主要考查棱锥,线面关系、直线与平面所成的角、点到面的距离等基本知识,同时考查空间想象能力和推理、运算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




 、
、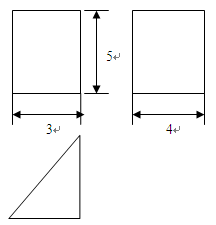




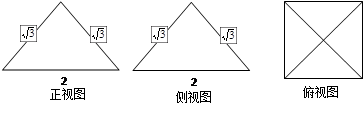
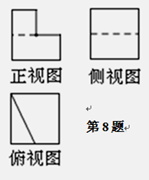
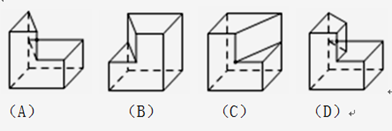




 的边长为
的边长为 ,它是水平放置的一个平面图形的直观图,则原图形的周长是
,它是水平放置的一个平面图形的直观图,则原图形的周长是 