题目内容
定义运算:x?y=
,例如:3?4=3,(-2)?4=4,则函数f(x)=x2?(2x-x2)的最大值为 .
|
分析:根据新定义,求出f(x)的表达式,然后利用数形结合求出函数f(x)的最大值即可.
解答:解:由x2=2x-x2,得x2=x,解得x=0或x=1,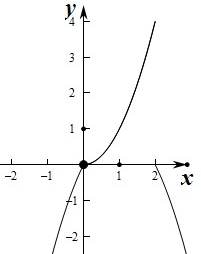
由y=2x-x2≥0,得0≤x≤2,
由y=2x-x2<0,得x<0或x>2,
∴由x2(2x-x2)≥0时,
解得0≤x≤2,
由x2(2x-x2)<0
解得x<0或x>2,
即当0≤x≤2时,f(x)=x2,
当x<0或x>2时,f(x)=2x-x2.
作出对应的函数图象
∴图象可知当x=2时,函数f(x)取得最大值f(2)=4.
故答案为:4.

由y=2x-x2≥0,得0≤x≤2,
由y=2x-x2<0,得x<0或x>2,
∴由x2(2x-x2)≥0时,
解得0≤x≤2,
由x2(2x-x2)<0
解得x<0或x>2,
即当0≤x≤2时,f(x)=x2,
当x<0或x>2时,f(x)=2x-x2.
作出对应的函数图象
∴图象可知当x=2时,函数f(x)取得最大值f(2)=4.
故答案为:4.
点评:本题主要考查函数的图象和性质,根据新定义求出函数的表达式是解决本题的关键,利用数形结合是解决本题的突破点.

练习册系列答案
相关题目
定义运算:x?y=
例如3?4=4,则下列等式不能成立 的是( )
|
| A、x?y=y?x |
| B、(x?y)?z=x?(y?z) |
| C、(x?y)2=x2?y2 |
| D、c•(x?y)=(c•x)?(c•y)(其中c为常数) |
定义运算:x?y=
则(x2-1)?(x+5),(x∈R)的最小值是( )
|
| A、1 | B、2 | C、3 | D、8 |