题目内容
14、在R上定义运算?:x?y=x(2-y),若不等式(x+m)?x<1对一切实数x恒成立,则实数m的取值范围是
(-4,0)
.分析:根据运算的定义得到不等式的具体形式:(x+m)(2-x)<1,进而整理不等式得到:x2+(m-2)x+(1-2m)>0,由该不等式对一切实数均成立,所以该一元二次不等式所对应的一元二次方程的判别式△<0,便可解得m的范围.
解答:解:由题意得:(x+m)?x=(x+m)(2-x)<1,
变形整理得:x2+(m-2)x+(1-2m)>0,
因为对任意的实数x不等式都成立,
所以其对应的一元二次方程:x2+(m-2)x+(1-2m)=0的根的判别式△=(m-2)2-4(1-2m)<0,解得:-4<m<0.
变形整理得:x2+(m-2)x+(1-2m)>0,
因为对任意的实数x不等式都成立,
所以其对应的一元二次方程:x2+(m-2)x+(1-2m)=0的根的判别式△=(m-2)2-4(1-2m)<0,解得:-4<m<0.
点评:本题考查一元二次不等式的解法.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 :x
:x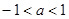 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.