题目内容
(本题满分14分)
设直线 与抛物线
与抛物线 交于不同两点A、B,F为抛物线的焦点。
交于不同两点A、B,F为抛物线的焦点。
(1)求 的重心G的轨迹方程;
的重心G的轨迹方程;
(2)如果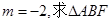 的外接圆的方程。
的外接圆的方程。
【答案】
① ;②
;② 。
。
【解析】
试题分析:(1)设出A、B、G的坐标,联立直线与抛物线,利用重心坐标公式,即可求得重心G的轨迹方程;
(2)确定AB的中垂线方程为x+y-6=0,令△ABF外接圆圆心为C(a,6-a),求出弦AB的长,C到AB的距离,利用|CA|=|CF|,即可求得圆心坐标与半径,从而可得△ABF的外接圆的方程。
解①设 ,
,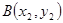 ,
, ,重心
,重心 ,
,
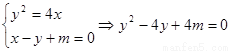 ∴△>0
∴△>0
 <1且
<1且 (因为A、B、F不共线)
(因为A、B、F不共线)
故
∴重心G的轨迹方程为 ………6分(范围不对扣1分)
………6分(范围不对扣1分)
② ,则
,则 ,设
,设 中点为
中点为
∴ ∴
∴
那么AB的中垂线方程为 ,令△ABF外接圆圆心为
,令△ABF外接圆圆心为
又 ,C到AB的距离为
,C到AB的距离为
∴
 ∴
∴ ∴
∴
∴所求的圆的方程为 ………14分
………14分
考点:本试题主要考查了轨迹方程,考查圆的方程,属于中档题
点评:解决该试题的关键是确定圆的圆心与半径。利用三角形的重心坐标公式及利用待定系数法求解圆的方程,主要体现了方程思想的应用。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).