Question

【题目】在三棱锥中，和均为边长为3的等边三角形，且，则三棱锥外接球的体枳为（ ）

A. B. C. D.

Answer 1

【答案】C

【解析】分析：先过△ABC的外心作平面PBC的垂线，过△PBC的外心作平面PBC的垂线，设两条垂线交于点O,则O为三棱锥P-ABC外接球的球心.再求出,，再解△得到外接球的半径R=OA=，最后求三棱锥P-ABC外接球的体积.

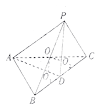
详解：取BC的中点D,连接PD,AD,因为△ABC和△PBC均为等边三角形，

所以AD⊥BC,PD⊥BC,AD∩PD=D,所以BC⊥平面PAD，

因为△ABC和△PBC均为边长为3的等边三角形，

所以AD=PD=,

又因为,所以PD⊥AD,

过△ABC的外心作平面PBC的垂线，过△PBC的外心作平面PBC的垂线，

设两条垂线交于点O,则O为三棱锥P-ABC外接球的球心.

,,

所以,

所以外接球的半径R=OA=,

所以三棱锥P-ABC外接球的体积.

故选C.