题目内容
（2006•宣武区一模）正四面体A-BCD中，E在棱AB上，F在棱CD上，使得
=
=λ(λ＞0)，设f（λ）=αλ+βλ，αλ与βλ分别表示EF与AC，BD所成的角，则（ ）
| AE |
| EB |
| CF |
| FD |
分析：先证明正四面体的对棱AC与BD垂直，此结论由线面垂直得来，再由异面直线所成的角的定义，在同一平面内找到αλ与βλ，最后在三角形中发现f（λ）=αλ+βλ=
，从而做出正确选择
| π |
| 2 |
解答：解：如图，取线段BC上一点H，使
=λ，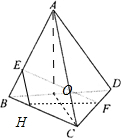
取BD中点O，连接AO，CO
∵正四面体A-BCD中每个面均为正三角形，∴BD⊥AO，BD⊥CO，∵AO∩CO=O，∴BD⊥平面AOC，∵AC?平面AOC∴BD⊥AC
∵
=λ(λ＞0)，
=λ，∴EH∥AC，∵
=λ(λ＞0)，
=λ，∴HF∥BD
∴∠HEF就是异面直线EF与AC所成的角，∠HFE就是异面直线EF与BD所成的角，∴∠EHF就是异面直线BD与AC所成的角，
∴αλ=∠HEF，βλ=∠HFE，∠EHF=90°
∴f（λ）=αλ+βλ=
，即f（λ）是（0，+∞）上的常数函数
故选D
| CH |
| HB |
取BD中点O，连接AO，CO∵正四面体A-BCD中每个面均为正三角形，∴BD⊥AO，BD⊥CO，∵AO∩CO=O，∴BD⊥平面AOC，∵AC?平面AOC∴BD⊥AC
∵
| AE |
| EB |
| CH |
| HB |
| CF |
| FD |
| CH |
| HB |
∴∠HEF就是异面直线EF与AC所成的角，∠HFE就是异面直线EF与BD所成的角，∴∠EHF就是异面直线BD与AC所成的角，
∴αλ=∠HEF，βλ=∠HFE，∠EHF=90°
∴f（λ）=αλ+βλ=
| π |
| 2 |
故选D
点评：本题考察了异面直线所成的角的作法和算法，正四面体的性质，解题时要认真体会将空间问题转化为平面问题的过程
练习册系列答案
相关题目