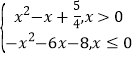题目内容
【题目】已知函数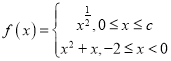 ,
,
其中c>0.那么f(x)的零点是________;若f(x)的值域是![]() ,则c的取值范围是________.
,则c的取值范围是________.
【答案】-1和0 (0,4]
【解析】
根据分段函数的概念,分x为正数和负数两种情况讨论,分别解方程即可得到么f(x)的零点.
根据二次函数的图象与性质,求出当x∈[-2,0)时,函数f(x)的值域恰好是[![]() ,2],所以当0≤x≤c时,f(x)=
,2],所以当0≤x≤c时,f(x)=![]() 的最大值小于等于2,即可解出实数c的取值范围.
的最大值小于等于2,即可解出实数c的取值范围.
当x≥0时,令![]() =0,得x=0;
=0,得x=0;
当x<0时,令x2+x=0,得x=-1或x=0(舍去)
∴f(x)的零点是-1和0
∵函数y=x2+x=![]() ,在区间[-2,-
,在区间[-2,-![]() )上是减函数,在区间(-
)上是减函数,在区间(-![]() ,0)上是增函数
,0)上是增函数
∴当x∈[-2,0)时,函数f(x)最小值为f(-![]() )=-
)=-![]() ,最大值是f(-2)=2
,最大值是f(-2)=2
∵当0≤x≤c时,f(x)=![]() 是增函数且值域为[0,
是增函数且值域为[0,![]() ]
]
∵f(x)的值域是[![]() ,2],∴
,2],∴ ![]() ≤2,即0<c≤4
≤2,即0<c≤4

练习册系列答案
相关题目