题目内容
已知向量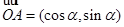 ,
,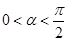 .向量
.向量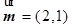 ,
,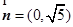 ,且
,且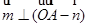 .
.
(1)求向量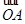 ;
;
(2)若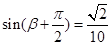 ,
,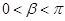 ,求
,求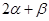 的值.
的值.
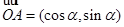 ,
,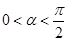 .向量
.向量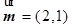 ,
,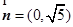 ,且
,且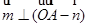 .
.(1)求向量
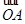 ;
;(2)若
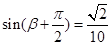 ,
,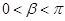 ,求
,求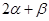 的值.
的值.(1)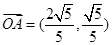 ;(2)
;(2) .
.
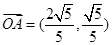 ;(2)
;(2) .
.(1)根据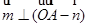 ,可得
,可得 ,从而可确定
,从而可确定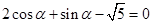 ,再根据
,再根据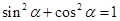 ,两方程联立解方程组即可求解.
,两方程联立解方程组即可求解.
(2)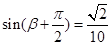 ,可得
,可得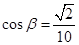 ,由第一问知
,由第一问知 ,
,
所以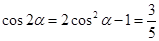 ,进而求出
,进而求出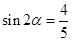 ,
,
∴ ,
,
下面关键是对角的范围进行分析可确定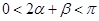
从而可知 .
.
解:(Ⅰ)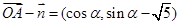 , ……………………………1分
, ……………………………1分
又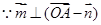 ,∴
,∴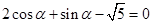 ,即
,即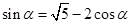 ,① …2分
,① …2分
又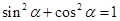 ②将①代入②中,可得
②将①代入②中,可得 ③ …4分
③ …4分
将③代入①中,得 …5分∴
…5分∴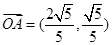 ………6分
………6分
(Ⅱ) ∵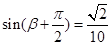 ,
,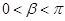 ,∴
,∴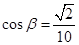 ,且
,且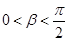 …7分
…7分
∴ . …………8分
. …………8分
由(Ⅰ)知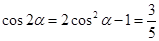 ,
,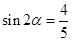 . ……10分
. ……10分
∴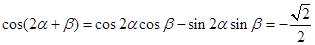 …………12分
…………12分
∵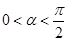 ,且注意到
,且注意到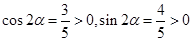 ,
,
∴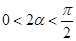 ,又
,又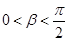 ,∴
,∴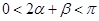 ......13分
......13分
综上可得 …………………14分
…………………14分
(若用 ,又∵
,又∵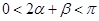 ∴
∴  ,酌情扣1分.)
,酌情扣1分.)
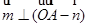 ,可得
,可得 ,从而可确定
,从而可确定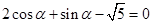 ,再根据
,再根据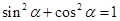 ,两方程联立解方程组即可求解.
,两方程联立解方程组即可求解.(2)
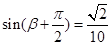 ,可得
,可得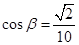 ,由第一问知
,由第一问知 ,
,所以
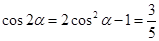 ,进而求出
,进而求出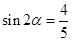 ,
,∴
 ,
,下面关键是对角的范围进行分析可确定
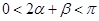
从而可知
 .
.解:(Ⅰ)
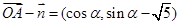 , ……………………………1分
, ……………………………1分又
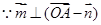 ,∴
,∴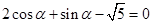 ,即
,即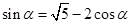 ,① …2分
,① …2分又
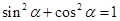 ②将①代入②中,可得
②将①代入②中,可得 ③ …4分
③ …4分将③代入①中,得
 …5分∴
…5分∴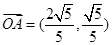 ………6分
………6分(Ⅱ) ∵
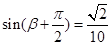 ,
,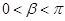 ,∴
,∴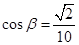 ,且
,且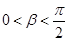 …7分
…7分∴
 . …………8分
. …………8分由(Ⅰ)知
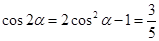 ,
,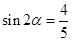 . ……10分
. ……10分∴
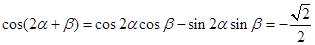 …………12分
…………12分∵
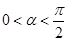 ,且注意到
,且注意到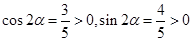 ,
,∴
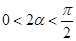 ,又
,又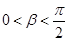 ,∴
,∴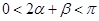 ......13分
......13分综上可得
 …………………14分
…………………14分(若用
 ,又∵
,又∵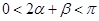 ∴
∴  ,酌情扣1分.)
,酌情扣1分.)
练习册系列答案
相关题目
 为周期的偶函数是( ).
为周期的偶函数是( ).



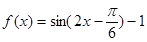 ;
; 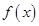 的单调递增区间;
的单调递增区间; 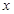
 求函数
求函数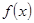 的最值及对应的
的最值及对应的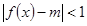 在
在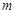 的取值范围.
的取值范围.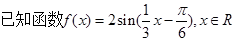 (13分)
(13分)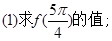
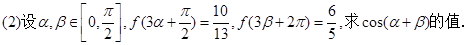
 ( )
( )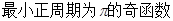



 )
)  )
)
 ,则
,则 ( )
( )

 或
或
 或
或 的最大值和最小值分别为
的最大值和最小值分别为 ,则
,则
 的定义域是___________________________
的定义域是___________________________