题目内容
已知函数f (x) = 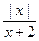
(1)判断函数f (x)在区间(0, +∞)上的单调性,并加以证明;
(2)如果关于x的方程f (x) = kx2有四个不同的实数解,求实数k的取值范围.
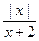
(1)判断函数f (x)在区间(0, +∞)上的单调性,并加以证明;
(2)如果关于x的方程f (x) = kx2有四个不同的实数解,求实数k的取值范围.
(1)单调递增函数(2)当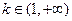 时,方程
时,方程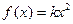 有四个不同的实数解
有四个不同的实数解
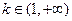 时,方程
时,方程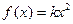 有四个不同的实数解
有四个不同的实数解(1)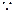
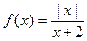 ,
,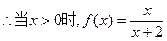 .
.
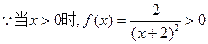 …………………………2分
…………………………2分
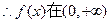 上单调递增函数.……………………4分
上单调递增函数.……………………4分
(2)原方程即:
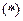
①
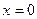 恒为方程
恒为方程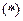 的一个解.……………………5分
的一个解.……………………5分
②当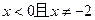 时方程
时方程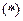 有解,则
有解,则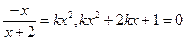
当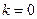 时,方程
时,方程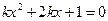 无解;
无解;
当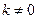 时,
时,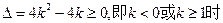 ,方程
,方程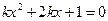 有解.
有解.
设方程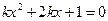 的两个根分别是
的两个根分别是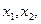 则
则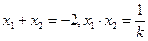 .
.
当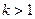 时,方程
时,方程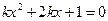 有两个不等的负根;…………………7分
有两个不等的负根;…………………7分
当 时,方程
时,方程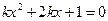 有两个相等的负根;………………9分.
有两个相等的负根;………………9分.
当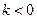 时,方程
时,方程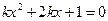 有一个负根………………………11分
有一个负根………………………11分
③当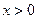 时,方程
时,方程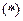 有解,则
有解,则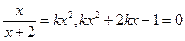
当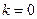 时,方程
时,方程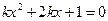 无解;
无解;
当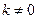 时,
时,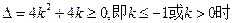 ,方程
,方程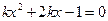 有解.
有解.
设方程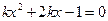 的两个根分别是
的两个根分别是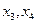
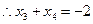 ,
,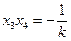
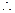 当
当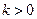 时,方程
时,方程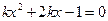 有一个正根,
有一个正根,
当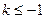 时,方程
时,方程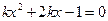 没有正根.……………………13分.
没有正根.……………………13分.
综上可得,当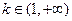 时,方程
时,方程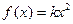 有四个不同的实数解.……16分.
有四个不同的实数解.……16分.
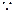
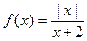 ,
,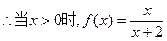 .
.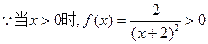 …………………………2分
…………………………2分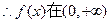 上单调递增函数.……………………4分
上单调递增函数.……………………4分(2)原方程即:

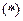
①

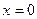 恒为方程
恒为方程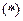 的一个解.……………………5分
的一个解.……………………5分②当
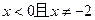 时方程
时方程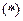 有解,则
有解,则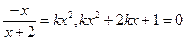
当
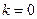 时,方程
时,方程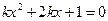 无解;
无解;当
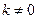 时,
时,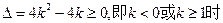 ,方程
,方程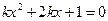 有解.
有解.设方程
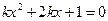 的两个根分别是
的两个根分别是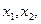 则
则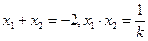 .
.当
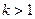 时,方程
时,方程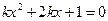 有两个不等的负根;…………………7分
有两个不等的负根;…………………7分当
 时,方程
时,方程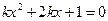 有两个相等的负根;………………9分.
有两个相等的负根;………………9分.当
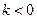 时,方程
时,方程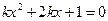 有一个负根………………………11分
有一个负根………………………11分③当
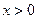 时,方程
时,方程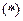 有解,则
有解,则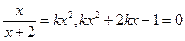
当
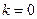 时,方程
时,方程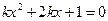 无解;
无解;当
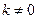 时,
时,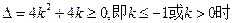 ,方程
,方程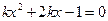 有解.
有解.设方程
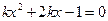 的两个根分别是
的两个根分别是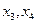
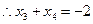 ,
,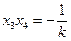
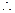 当
当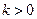 时,方程
时,方程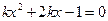 有一个正根,
有一个正根,当
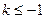 时,方程
时,方程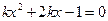 没有正根.……………………13分.
没有正根.……………………13分.综上可得,当
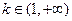 时,方程
时,方程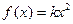 有四个不同的实数解.……16分.
有四个不同的实数解.……16分.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 和
和 ,它们的交点是P(
,它们的交点是P( ),若曲线C的方程为
),若曲线C的方程为
 +
+
 ="0" (
="0" ( 0时曲线C经过点P
0时曲线C经过点P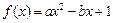 .
.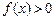 的解集是
的解集是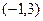 ,求实数
,求实数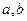 的值;
的值;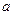 为整数,
为整数,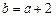 ,且函数
,且函数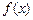 在
在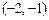 上恰有一个零点,求
上恰有一个零点,求 存在反函数
存在反函数 ,方程
,方程 =0的解集是P,方程
=0的解集是P,方程 Q;
Q; .
.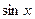 =
=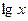 的实根有 ( )
的实根有 ( ) 在区间
在区间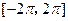 上的零点个数是( )
上的零点个数是( )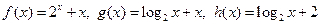 的零点依次为
的零点依次为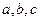 ,则( )
,则( )


