题目内容
在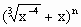 的展开式中,第5、6、7项的系数成等差数列,求展开式中不含x的项.
的展开式中,第5、6、7项的系数成等差数列,求展开式中不含x的项.
答案:
解析:
解析:
|
解依题意,得
化简得 ∴ n=7,n=14. 当n=7时,设展开式中不含x的项为第r+1项,则
令 ∴ 当n=14时,同理可得
令 ∴ 注意,不知二项式的次数,求二项展开式的某一项,需先根据已知条件确定二项式的次数n,再运用通项公式求解. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
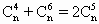 ,且n≥6.
,且n≥6.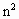 -21n+98=0.
-21n+98=0.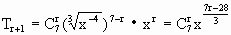 .
.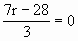 =0,解得r=4.
=0,解得r=4. =
= =35为所求.
=35为所求.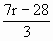 =0,解得r=8.
=0,解得r=8. =3003即为所求.
=3003即为所求.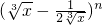 的展开式中,第5项为常数项.
的展开式中,第5项为常数项.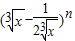 的展开式中,第5项为常数项.
的展开式中,第5项为常数项.