题目内容
已知在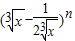 的展开式中,第5项为常数项.
的展开式中,第5项为常数项.(1)求n;
(2)求展开式中含x2的项.
【答案】分析:(1)先求出 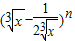 的展开式的通项公式为Tr+1=
的展开式的通项公式为Tr+1=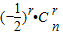 •
• ,再令r=4,可得第5项,再由第5项为常数项求得n的值.
,再令r=4,可得第5项,再由第5项为常数项求得n的值.
(2)由(1)可得展开式的通项公式中,令x的幂指数 =2,解得r=1,从而求得展开式中含x2的项.
=2,解得r=1,从而求得展开式中含x2的项.
解答:解:(1)由于 的展开式的通项公式为Tr+1=
的展开式的通项公式为Tr+1= •
• •
•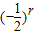 •
• =
= •
• ,
,
故第5项为 T4+1= •
•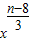 .
.
由于第5项为常数项,∴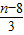 =0,解得 n=8.
=0,解得 n=8.
(2)由(1)可得展开式的通项公式为Tr+1=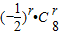 •
•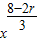 ,令
,令 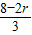 =2,解得r=1,
=2,解得r=1,
故展开式中含x2的项为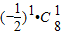 •x2=-4x2.
•x2=-4x2.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于中档题.
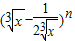 的展开式的通项公式为Tr+1=
的展开式的通项公式为Tr+1=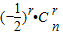 •
• ,再令r=4,可得第5项,再由第5项为常数项求得n的值.
,再令r=4,可得第5项,再由第5项为常数项求得n的值.(2)由(1)可得展开式的通项公式中,令x的幂指数
 =2,解得r=1,从而求得展开式中含x2的项.
=2,解得r=1,从而求得展开式中含x2的项.解答:解:(1)由于
 的展开式的通项公式为Tr+1=
的展开式的通项公式为Tr+1= •
• •
•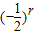 •
• =
= •
• ,
,故第5项为 T4+1=
 •
•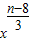 .
.由于第5项为常数项,∴
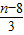 =0,解得 n=8.
=0,解得 n=8.(2)由(1)可得展开式的通项公式为Tr+1=
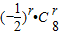 •
•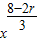 ,令
,令 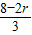 =2,解得r=1,
=2,解得r=1,故展开式中含x2的项为
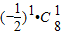 •x2=-4x2.
•x2=-4x2.点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 的展开式中,第6项
的展开式中,第6项 为常数项.
为常数项. 的展开式中,第7项为常数项,
的展开式中,第7项为常数项, 的展开式中,第4项为常数项
的展开式中,第4项为常数项 的值; (2) 求展开式中含
的值; (2) 求展开式中含 项系数.
项系数. 的展开式中,第6项为常数项.
的展开式中,第6项为常数项. 的项的系数;
的项的系数;