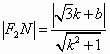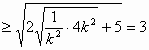题目内容

已知F1(，0)，F2(，0)，动点P满足|PF1|＋|[PF2|＝4，记动点P的轨迹为E．

(Ⅰ)求E的方程．

(Ⅱ)曲线E的一条切线l，过F1，F2作l发的垂线，垂足分别为M，N，求|F1M|·|F2N|的值．

(Ⅲ)曲线E的一条切线为l，与x轴，y分别交于A，B两点，求|AB|的最小值，并求此时切线的斜率．

答案：
解析：

　　解：(Ⅰ)

　　又

　　点轨迹是以为焦点的椭圆，，

　　故椭圆方程为　3分

　　(Ⅱ)①当切线斜率不存在时，切线为，此时　4分

　　②当切线斜率存在时，设切线方程为

　　

　　，　6分

　　，

　　，故　8分

　　(Ⅲ)由(Ⅱ)知，

　　　10分

　　

　　当且仅当，即时取等号

　　故的最小值为3，此时斜率为　12分


练习册系列答案
相关题目
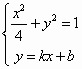
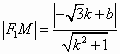已知函数f（x）的图象在[a，b]上连续不断，定义：f1（x）=min{f（t）|a≤t≤x}（x∈[a，b]），f2（x）=max{f（t）|a≤t≤x}（x∈[a，b]）．其中，min{f（x）|x∈D}表示函数f（x）在D上的最小值，max{f（x）|x∈D}表示函数f（x）在D上的最大值．若存在最小正整数k，使得f2（x）-f1（x）≤k（x-a）对任意的x∈[a，b]成立，则称函数f（x）为[a，b]上的“k阶收缩函数”．
（1）若f（x）=cosx，x∈[0，π]，试写出f1（x），f2（x）的表达式；
（2）已知函数f（x）=x2，x∈[-1，4]，试判断f（x）是否为[-1，4]上的“k阶收缩函数”，如果是，求出对应的k；如果不是，请说明理由；
（3）已知b＞0，函数f（x）=-x3+3x2是[0，b]上的2阶收缩函数，求b的取值范围．
已知f1（x）=|3x-1|，f2（x）=|a•3x-9|（a＞0），x∈R，且f(x)=
f1(x)     f1(x)≤f2(x)   
f2(x)     f1(x)＞f2(x)
．
（Ⅰ）当a=1时，求f（x）在x=1处的切线方程；
（Ⅱ）当2≤a＜9时，设f（x）=f2（x）所对应的自变量取值区间的长度为l（闭区间[m，n]的长度定义为n-m），试求l的最大值；
（Ⅲ）是否存在这样的a，使得当x∈[2，+∞）时，f（x）=f2（x）？若存在，求出a的取值范围；若不存在，请说明理由．
已知双曲线C：
x2
a2
-
y2
b2
=1 (a＞0，b＞0)的两个焦点为F1（-2，0），F2（2，0），点(3，
7
)在双曲线C上．
（1）求双曲线C的方程；
（2）已知Q（0，2），P为双曲线C上的动点，点M满足
QM
=
MP
，求动点M的轨迹方程；
（3）过点Q（0，2）的直线l与双曲线C相交于不同的两点E、F，记O为坐标原点，若△OEF的面积为2
2
，求直线l的方程．
已知F1，F2是椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的焦点，过F1的直线l交C于A，B两点，且△ABF2的周长为8，C上的动点到焦点距离的最小值为1，
（1）求椭圆C的方程；
（2）若点P是椭圆C上不与椭圆顶点重合的任意一点，点M是椭圆C上不与椭圆顶点重合且异于点P的任意一点，点M关于x轴的对称点是点N，直线MP，NP分别交x轴于点E（x1，0），点F（x2，0），探究x1•x2是否为定值，若为定值，求出该定值，若不为定值，请说明理由．

已知函数f(x)的图象在[a，b]上连续不断，定义：

，

其中，min{f(x)|x∈D}表示函数f(x)在区间上的最小值，max{f(x)|x∈D}表示函数f(x)在区间上的最大值．若存在最小正整数k，使得f2(x)－f1(x)≤k(x－a)对任意的x∈[a，b]成立，则称函数为区间[a，b]上的“k阶收缩函数”．

(1)若f(x)＝cosx，x∈[0，π]，试写出f1(x)，f2(x)的表达式；

(2)已知函数f(x)＝x2，x∈[－1，4]，试判断f(x)是否为[－1，4]上的“k阶收缩函数”，如果是，求出相应的k；如果不是，请说明理由；

(3)已知b＞0函数f(x)＝－x3＋3x2是[0，b]上的2阶收缩函数，求b的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网