题目内容
已知三棱锥P-ABC的底面是以AB为斜边的等腰直角三角形,AB=PA=PB=PC=10,则该三棱锥的外接球的球心到平面ABC的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、5
|
考点:球的体积和表面积
专题:空间位置关系与距离
分析:根据三棱锥P-ABC的底面是以AB为斜边的等腰直角三角形,AB=PA=PB=PC=10,可得P在面ABC上的射影为AB中点H,PH⊥平面ABC,在面PHC内作PC的垂直平分线MO与PH交于O,则O为PABC的外接球球心,OH为O与平面ABC的距离,由此可得结论.
解答:
解:∵三棱锥P-ABC的底面是以AB为斜边的等腰直角三角形,AB=PA=PB=PC=10,如图
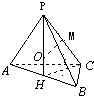
∴P在面ABC上的射影为AB中点H,
∴PH⊥平面ABC.
∴PH上任意一点到A、B、C的距离相等.
∵PA=PB=PC=10
∴PH=5
,CH=5,
在面PHC内作PC的垂直平分线MO与PH交于O,则OP=OC=OA=OB,所以O为PABC的外接球球心.
∵PA=PB=AB=10,
∴PO=
,∴OH=
,即为O与平面ABC的距离.
故选B.

∴P在面ABC上的射影为AB中点H,
∴PH⊥平面ABC.
∴PH上任意一点到A、B、C的距离相等.
∵PA=PB=PC=10
∴PH=5
| 3 |
在面PHC内作PC的垂直平分线MO与PH交于O,则OP=OC=OA=OB,所以O为PABC的外接球球心.
∵PA=PB=AB=10,
∴PO=
10
| ||
| 3 |
5
| ||
| 3 |
故选B.
点评:本题考查点到面的距离的计算,考查学生分析解决问题的能力,确定OHO与平面ABC的距离是关.键

练习册系列答案
相关题目
方程sin2x+cosx+k=0有解,则k的范围是( )
A、-
| ||
B、-
| ||
C、0≤k≤
| ||
D、-1≤k≤
|
已知等差数列{an}的前n项和为Sn,若
=a10
+a11
,且A、B、C三点共线(该直线不过点O),则S20=( )
| OB |
| OA |
| OC |
| A、10 | B、11 | C、20 | D、21 |
把77化成四进制数的末位数字为( )
| A、1 | B、2 | C、3 | D、4 |
若集合A={x||x|=x},B={x|x2+x≥0},则A∩B=( )
| A、[-1,0] |
| B、[0,+∞) |
| C、[1,+∞) |
| D、(-∞,-1] |