题目内容
(2005•东城区一模)已知向量
=(2sinx,cosx),
=(
cosx,2cosx),定义函数f(x)=
•
-1.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调减区间;
(3)画出函数g(x)=f(x),x∈[-
,
]的图象,由图象研究并写出g(x)的对称轴和对称中心.

| a |
| b |
| 3 |
| a |
| b |
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调减区间;
(3)画出函数g(x)=f(x),x∈[-
| 7π |
| 12 |
| 5π |
| 12 |

分析:(1)利用二倍角公式和两角和公式对函数的解析式进行化简整理,然后利用周期公式求得函数的最小正周期;
(2)利用正弦函数的性质求得函数单调减时2x+
的范围,进而求得x的范围即函数的单调减区间;
(3)用五点法作出g(x)的图象,结合图象研究g(x)的对称轴和对称中心.
(2)利用正弦函数的性质求得函数单调减时2x+
| π |
| 6 |
(3)用五点法作出g(x)的图象,结合图象研究g(x)的对称轴和对称中心.
解答:解:f(x)=
•
-1=2
sinxcosx+2cos2x-1
=
sin2x+cos2x=2sin(2x+
).…(5分)
(1)f(x)的最小正周期T=
=π.…(6分)
(2)由2kπ+
≤2x+
≤2kπ+
?2kπ+
≤2x≤2kπ+
?kπ+
≤x≤kπ+
(k∈Z).
∴函数f(x)的单调减区间为[kπ+
,kπ+
](k∈Z).…(9分)
(3)函数g(x)=f(x),x∈[-
,
]的图象如图所示,
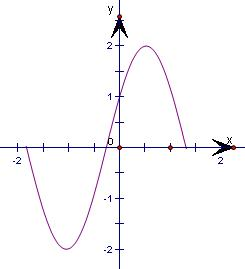
从图象上可以直观看出,此函数没有对称轴,有一个对称中心.
∴对称中心是(-
,0)…(14分)
| a |
| b |
| 3 |
=
| 3 |
| π |
| 6 |
(1)f(x)的最小正周期T=
| 2π |
| |ω| |
(2)由2kπ+
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 3 |
| 4π |
| 3 |
?kπ+
| π |
| 6 |
| 2π |
| 3 |
∴函数f(x)的单调减区间为[kπ+
| π |
| 6 |
| 2π |
| 3 |
(3)函数g(x)=f(x),x∈[-
| 7π |
| 12 |
| 5π |
| 12 |

从图象上可以直观看出,此函数没有对称轴,有一个对称中心.
∴对称中心是(-
| π |
| 12 |
点评:本题主要考查平面向量数量积的运算、二倍角公式和两角和与差的公式的应用和正弦函数的基本性质,考查基础知识的综合应用,三角函数的公式比较多,平时一定要加强记忆,到运用时方能做到游刃有余.

练习册系列答案
相关题目