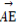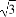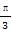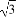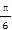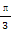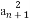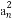Question

在数列{an}中,a1=1,an+1=can+cn+1(2n+1)(n∈N*),其中实数c≠0.求{an}的通项公式.

 

Answer 1

an=(n2-1)cn+cn-1,n∈N*

【解析】由原式得=+(2n+1).令bn=,

则b1=,bn+1=bn+(2n+1),

因此对n≥2有bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1=(2n-1)+(2n-3)+…+3+=n2-1+,

因此an=(n2-1)cn+cn-1,n≥2.

又当n=1时上式成立.

因此an=(n2-1)cn+cn-1,n∈N*.