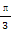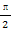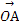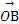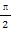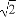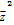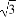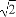题目内容
已知函数f(x)=cos2(x-
)-sin2x.
(1)求f(
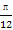)的值.
(2)若对于任意的x∈[0,
],都有f(x)≤c,求实数c的取值范围.
(1) 
(2) [,+∞)
【解析】(1)f(
)=cos2(-)-sin2=cos
=.
(2)f(x)=
[1+cos(2x-
)]-(1-cos2x)
=[cos(2x-)+cos2x]
=(sin2x+
cos2x)
=sin(2x+).
因为x∈[0,
],所以2x+∈[,
],
所以当2x+=,即x=时,f(x)取得最大值.
所以对于任意的x∈[0,],f(x)≤c等价于≤c.
故对于任意的x∈[0,],都有f(x)≤c时,c的取值范围是[,+∞).
练习册系列答案
53随堂测系列答案
相关题目
