题目内容
已知U={x|x2-3x+2≥0},A={x||x-2|>1},B={x|≥0},求A∩B,A∪B,
(CUA)∪B,A∩(CUB).
(CUA)∪B,A∩(CUB).
∵U={x|x2-3x+2≥0}={x|(x-2)(x-1)≥0}={x|x≥2或x≤1},A={x||x-2|>1}
={x|x-2>1或x-2<-1}={x|x>3或x<1},
B={x|}={x|x>2或x≤1}.由图(1)可知,A∩B={x|x>3或x<1},A∪B={x|x>2或x≤1}.

由图(2)可知CUA={x|2≤x≤3或x=1},易知CUB={x|x=2}.
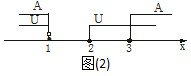
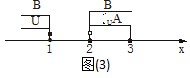
由图(3)可知,(CUA)∪B={x|x≥2或x≤1}=U.
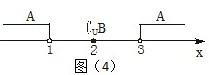
由图(4)可知,A∩(CUB)=∅.
={x|x-2>1或x-2<-1}={x|x>3或x<1},
B={x|}={x|x>2或x≤1}.由图(1)可知,A∩B={x|x>3或x<1},A∪B={x|x>2或x≤1}.

由图(2)可知CUA={x|2≤x≤3或x=1},易知CUB={x|x=2}.

由图(3)可知,(CUA)∪B={x|x≥2或x≤1}=U.

由图(4)可知,A∩(CUB)=∅.


练习册系列答案
相关题目