题目内容
若一三角形三边所在的直线方程分别为x+2y-5=0,y-2=0,x+y-4=0,则能够覆盖此三角形且面积最小的圆的方程为
x2+y2-3x-y=0
x2+y2-3x-y=0
.分析:确定三角形的三个顶点坐标,能够覆盖此三角形且面积最小是三角形的外接圆,利用待定系数法,即可求得结论.
解答:解:∵三角形三边所在的直线方程分别为x+2y-5=0,y-2=0,x+y-4=0,
∴可得三角形的三个顶点分别是(1,2),(2,2),(3,1)
能够覆盖此三角形且面积最小是三角形的外接圆,设方程为x2+y2+Dx+Ey+F=0,则
,∴
∴能够覆盖此三角形且面积最小的圆的方程为x2+y2-3x-y=0
故答案为:x2+y2-3x-y=0
∴可得三角形的三个顶点分别是(1,2),(2,2),(3,1)
能够覆盖此三角形且面积最小是三角形的外接圆,设方程为x2+y2+Dx+Ey+F=0,则
|
|
∴能够覆盖此三角形且面积最小的圆的方程为x2+y2-3x-y=0
故答案为:x2+y2-3x-y=0
点评:本题考查圆的方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
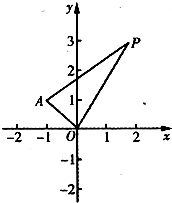 在平面直角坐标系xOy中,已知点A(一1,1),P是动点,且三角形POA的三边所在直线的斜率满足kOP+kOA=kPA.
在平面直角坐标系xOy中,已知点A(一1,1),P是动点,且三角形POA的三边所在直线的斜率满足kOP+kOA=kPA.