题目内容
(本小题满分16分)
已知数列 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)对任意给定的 ,是否存在
,是否存在 (
( )使
)使 成等差数列?若存在,用
成等差数列?若存在,用 分别表示
分别表示 和
和 (只要写出一组);若不存在,请说明理由;
(只要写出一组);若不存在,请说明理由;
(3)证明:存在无穷多个三边成等比数列且互不相似的三角形,其边长为 .
.
【解】(1)当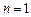 时,
时,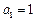 ;
;
当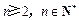 时,
时,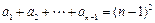 ,
,
所以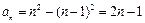 ;
;
综上所述,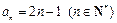 .…………………3分
.…………………3分
(2)当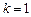 时,若存在p,r使
时,若存在p,r使 成等差数列,则
成等差数列,则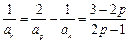 ,
,
因为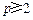 ,所以
,所以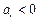 ,与数列
,与数列 为正数相矛盾,因此,当
为正数相矛盾,因此,当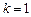 时不存在;…5分
时不存在;…5分
当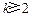 时,设
时,设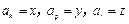 ,则
,则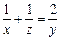 ,所以
,所以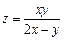 ,……………7分
,……………7分
令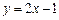 ,得
,得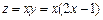 ,此时
,此时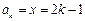 ,
, ,
,
所以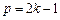 ,
,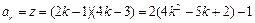 ,
,
所以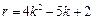 ;
;
综上所述,当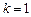 时,不存在p,r;当
时,不存在p,r;当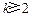 时,存在
时,存在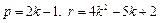 满足题设.
满足题设.
………………10分
(3)作如下构造: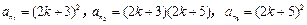 ,其中
,其中 ,
,
它们依次为数列 中的第
中的第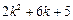 项,第
项,第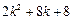 项,第
项,第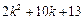 项…12分
项…12分
显然它们成等比数列,且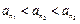 ,
,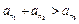 ,所以它们能组成三角形.
,所以它们能组成三角形.
由 的任意性,这样的三角形有无穷多个.…………………14分
的任意性,这样的三角形有无穷多个.…………………14分
下面用反证法证明其中任意两个三角形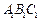 和
和 不相似:
不相似:
若三角形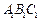 和
和 相似,且
相似,且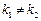 ,则
,则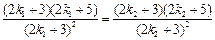 ,
,
整理得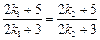 ,所以
,所以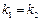 ,这与条件
,这与条件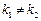 相矛盾,
相矛盾,
因此,任意两个三角形不相似.故命题成立.……………………16分
解析

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
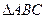 的内角
的内角 、
、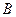 的对边分别为
的对边分别为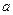 、
、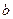 ,
,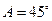 ,
,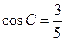 .
.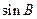 ;
;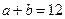 ,求
,求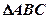 中,角
中,角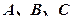 所对的边分别为
所对的边分别为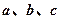 ,且满足
,且满足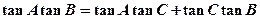 。
。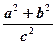 的值;
的值; 在双曲线
在双曲线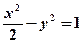 上,求
上,求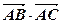 的值
的值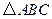 中,内角
中,内角 对边的边长分别是
对边的边长分别是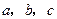 ,已知
,已知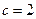 ,
,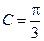 .
.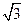 ,求
,求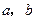 ;
;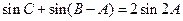 ,求
,求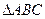 中,角
中,角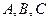 所对的边分别为
所对的边分别为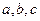 又
又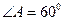 ,
,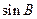 :
: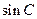 =2:3.
=2:3.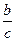 的值; (2)若
的值; (2)若 上的高为
上的高为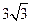 ,求a的值.
,求a的值.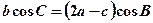
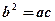 ,试确定△ABC的形状.
,试确定△ABC的形状.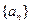 满足
满足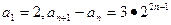 。
。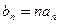 ,求数列
,求数列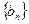 的
的 前
前 项和
项和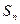
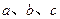 ,若
,若 ,求角
,求角 、角
、角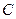 的大小。
的大小。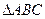 中,
中,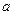 、
、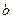 、
、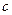 分别为角A、B、C的对边,且
分别为角A、B、C的对边,且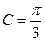 ,
,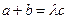 ,(其中
,(其中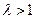 ).
). (Ⅰ)若
(Ⅰ)若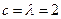 时,求
时,求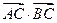 的值;
的值;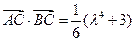 时,求边长
时,求边长