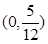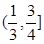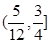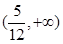题目内容
求经过点A(2-,2)并且和x轴的正半轴、y轴的正半轴所围成的三角形的面积是1的直线方程.
∵直线的斜率存在,
∴可设直线l的方程为:y-2=k(x+2).
即y=kx+2k+2.
令x=0,得y=2k+2;令y=0,
解得x=-
.
由
,解得-1<k<0.
∵S△=1,
∴
(2k+2)(-
)=1,
解得:k=-2或-
.
∵-1<k<0,∴k=-
.
∴直线l的方程为:x+2y-2=0.
∴可设直线l的方程为:y-2=k(x+2).
即y=kx+2k+2.
令x=0,得y=2k+2;令y=0,
解得x=-
| 2k+2 |
| k |
由
|
∵S△=1,
∴
| 1 |
| 2 |
| 2k+2 |
| k |
解得:k=-2或-
| 1 |
| 2 |
∵-1<k<0,∴k=-
| 1 |
| 2 |
∴直线l的方程为:x+2y-2=0.

练习册系列答案
相关题目
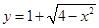
 与直线
与直线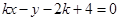 有两个相异的交点时,实数k的取值范围是( )
有两个相异的交点时,实数k的取值范围是( )