Question

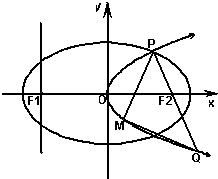如图，设抛物线C₁：y²=4mx（m＞0）的准线与x轴交于点F₁，焦点为F₂；以F₁，F₂为焦点，离心率为

1

2

的椭圆C₂与抛物线C₁在x轴上方的交点为P，延长PF₂交抛物线于点Q，M是抛物线C₁上一动点，且M在P与Q之间运动．
（1）当m=3时，求椭圆C₂的标准方程；
（2）若|PF₂|=5且P点横坐标为

2

3

m，求面积△MPQ的最大值．

Answer 1

分析：（1）：当m=3时，y²=12x，可设椭圆方程为

x2

a2

+

y2

b2

=1（a＞b＞0），结合已知可求c及e=

c

a

=

1

2

，可求a，再由b²=a²-c²可求b，进而可求椭圆方程
（2）由xp=

2m

3

及|PF₂|=xp+m=

5m

3

可求m，此时抛物线方程为y²=12x，F₂（3，0），P（2，2

6

），从而可求直线PQ的方程，联立

y=-2 6 (x-3) y2=12x

，可求Q（

9

2

，-3

6

），及PQ，设点M（

t2

12

，t）到直线PQ的距离为d，由题意可知t∈(-2

6

，2

6

)，由点到直线的距离公式可得d=

| 6 6 t2+t-6 6 |

24+1

=

6

30

|(t+

6

2

)2+

75

2

|，结合二次函数的性质可求d的最大，代入可求MPQ面积的最大值

解答：解：（1）：当m=3时，y²=12x，F₁（-3，0），F₂（3，0）…（1分）
设椭圆方程为

x2

a2

+

y2

b2

=1（a＞b＞0），则c=3，又e=

c

a

=

1

2

，所以a=6，b²=27
所以椭圆C₂方程为

x2

36

+

y2

27

=1（4分）
（2）∵xp=

2m

3

∴|PF₂|=xp+m=

5m

3

又|PF₂|=5∴m=3
此时抛物线方程为y²=12x，F₂（3，0），x_p=2…（6分）
又P在x轴上方，P（2，2

6

）
∴直线PQ的斜率为：KPF2=-2

6

∴直线PQ的方程为：y=-2

6

（x-3）…（8分）
联立 

y=-2 6 (x-3) y2=12x

，得2x²-13x+18=0
∵直线PQ的斜率为kPQ=-2

6

＜0，由图知x＞2
所以x=

9

2

代入抛物线方程得y=-3

6

，即Q（

9

2

，-3

6

）
PQ=

(2- 9 2 )2+(2 6 +3 6 )2

=

25

2

∵2x²-13x+18=0
∴x1+x2=

13

2

，x1x2=9
PQ=

1+(2 6 )2

|x1-x2|=5

(x1+x2)2-4x1x2

=5

( 13 2 )2-4×9

=

25

2

…（11分）
设点M（

t2

12

，t）到直线PQ的距离为d，
∵M在P与Q之间运动，∴t∈(-2

6

，2

6

)
d=

| 6 6 t2+t-6 6 |

24+1

=

6

30

|(t+

6

2

)2+

75

2

|
当t=-

6

2

，d_max=

6

30

•

75

2

=

5 6

4

   …（14分）
即MPQ面积的最大值为

1

2

×

25

2

×

5 6

4

=

125 6

16

      …（15分）

点评：本题考查直线与圆锥曲线的综合问题，解题时要认真审题，仔细解答，注意挖掘题设中的隐含条件．本题主要考查运算，整个题目的解答过程看起来非常繁琐，注意运算．