Question

（2008•临沂二模）在三棱锥S-ABC中，△ABC是边长为4的正三角形，SB=2

5

，SA=SC=2

3

，M、N分别是AB、SB的中点；
（1）证明：平面SAC⊥平面ABC；
（2）求直线MN与平面SBC所成角的正弦值．

Answer 1

分析：（1）取AC中点D，连SD，BD，证明SD⊥平面ABC，利用面面垂直的判定，可得平面SAC⊥平面ABC；
（2）建立坐标系，求出平面SCB的法向量，利用向量的夹角公式，即可求直线MN与平面SBC所成角的正弦值．

解答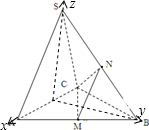：（1）证明：取AC中点D，连SD，BD，
∵SA=SC，∴SD⊥AC
∵△ABC是边长为4的正三角形，SB=2

5

，SA=SC=2

3

，
∴SD=2

2

，BD=2

3

∴SD⊥BD
∵AC∩BD=D
∴SD⊥平面ABC
∵SD?平面SAC
∴平面SAC⊥平面ABC；..（6分）
（2）解：以D为原点，DA为x轴，DB为y轴，DS为z轴建立空间直角坐标系，则A（2，0，0），C（-2，0，0），B(0，2

3

，0)，S(0，0，2

2

)，M(1，

3

，0)，N(0，

3

，

2

)
∴

MN

=(-1，0，

2

)，

CS

=(2，0，2

2

)，

CB

=(2，2

3

，0)
设平面SCB的法向量为

n

=(x，y，z)，则有

2x+2 2 z=0 2x+2 3 y=0

，
令x=1，得到

n

=(1，-

3

3

，-

2

2

)…．…..（8分）
设直线MN与平面SBC所成角为θ，则sinθ=|cos＜

n

，

MN

＞|=

2 22

11

…..（12分）

点评：本题以三棱锥为载体，考查线面垂直，面面垂直，考查线面角，考查向量知识的运用，属于中档题．