题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,直线
,直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知点![]() ,求证:若圆
,求证:若圆![]() 与直线
与直线![]() 相切,则圆
相切,则圆![]() 与直线
与直线![]() 也相切.
也相切.
【答案】(I)![]() ;(II)证明见解析.
;(II)证明见解析.
【解析】试题分析:(1)利用条件布列![]() 的方程组,即可得到椭圆
的方程组,即可得到椭圆![]() 的标准方程;(2)对直线l的斜率分类讨论,若圆
的标准方程;(2)对直线l的斜率分类讨论,若圆![]() 与直线
与直线![]() 相切,则圆
相切,则圆![]() 与直线
与直线![]() 也相切等价于
也相切等价于
![]() ,联立方程,借助根与系数关系证明等式即可.
,联立方程,借助根与系数关系证明等式即可.
试题解析:
(Ⅰ)设椭圆C的焦距为2c(c>0),依题意, 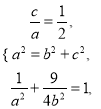
解得![]() ,c=1,故椭圆C的标准方程为
,c=1,故椭圆C的标准方程为![]() ;
;
(Ⅱ)证明:当直线l的斜率不存在时,直线l的方程为![]() ,M,N两点关于x轴对称,点P(4,0)在x轴上,所以直线PM与直线PN关于x轴对称,所以点O到直线PM与直线PN的距离相等,故若圆
,M,N两点关于x轴对称,点P(4,0)在x轴上,所以直线PM与直线PN关于x轴对称,所以点O到直线PM与直线PN的距离相等,故若圆![]() 与直线PM相切,则也会与直线PN相切;
与直线PM相切,则也会与直线PN相切;
当直线l的斜率存在时,设直线l的方程为![]() ,
, ![]() ,
, ![]() ,
,
由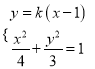 得:
得: ![]()
所以![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
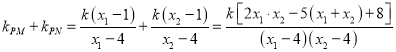
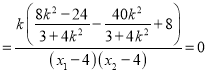 ,
,
所以, ![]() ,于是点O到直线PM与直线的距离PN相等,
,于是点O到直线PM与直线的距离PN相等,
故若圆![]() 与直线PM相切,则也会与直线PN相切;
与直线PM相切,则也会与直线PN相切;
综上所述,若圆![]() 与直线PM相切,则圆
与直线PM相切,则圆![]() 与直线PN也相切.
与直线PN也相切.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目