题目内容

3．已知区域M：$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$，定点A（3，1），在M内任取一点P，使得PA≥$\sqrt{2}$的概率为（　　）
A．$\frac{5}{2}-\frac{π}{8}$B．$\frac{5}{4}$-$\frac{π}{8}$C．$\frac{5}{2}-\frac{π}{4}$D．$\frac{5}{4}$

分析 由题意，画出区域M，和满足PA≥$\sqrt{2}$的部分，利用几何概型公式解答．

解答 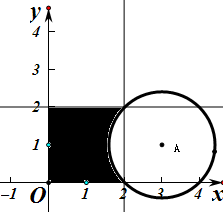解：如图区域M是边长为2的正方形，在M内任取一点P，使得PA≥$\sqrt{2}$的区域是图中阴影部分，面积为4-（$\frac{1}{4}π×2-\frac{1}{2}×\sqrt{2}×\sqrt{2}$）=5-$\frac{π}{2}$，
由几何概型公式可得在M内任取一点P，使得PA≥$\sqrt{2}$的概率为$\frac{5-\frac{π}{2}}{4}=\frac{5}{4}-\frac{π}{8}$；
故选B．

点评 本题考查了几何概型公式的运用，关键是求出使得PA≥$\sqrt{2}$的部分面积，利用几何概型公式求之．

练习册系列答案
相关题目
13．已知数列{an}的前n项和为Sn，且Sn=$\frac{1}{2}{n^2}$+$\frac{11}{2}$n（n∈N*）．
（1）求数列{an}的通项公式；
（2）设cn=$\frac{1}{{（2{a_n}-11）（2{a_n}-9）}}$，数列{cn}的前n项和为Tn，求使不等式Tn＞$\frac{k}{2015}$对一切n∈N*都成立的最大正整数k的值；
（3）设f（n）=$\left\{\begin{array}{l}{a_n}（n=2k-1，k∈{N^*}）\\ 3{a_n}-13（n=2k，k∈{N^*}）\end{array}$，是否存在m∈N*，使得f（m+15）=5f（m）成立？若存在，求出m的值；若不存在，请说明理由．
14．已知函数f（x）=$\sqrt{3}$sin（π-ωx）sin（$\frac{π}{2}$+ωx）+cos2ωx-$\frac{1}{2}$，ω＞0，其图象上相邻三个最值点构成的三角形的面积为π．
（1）求函数f（x）的最小正周期以及单调递增区间；
（2）设△ABC的内角A满足f（A）=1且$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\sqrt{3}$，求边BC的最小值．
11．设函数f（x）=lnx+$\frac{k}{x}$，k∈R．
（Ⅰ）若曲线y=f（x）在点（e，f（e））处的切线与直线x-2=0垂直，求k值；
（Ⅱ）若对任意x1＞x2＞0，f（x1）-f（x2）＜x1-x2恒成立，求k的取值范围；
（Ⅲ）已知函数f（x）在x=e处取得极小值，不等式f（x）＜$\frac{m}{x}$的解集为P，若M={x|e≤x≤3}，且M∩P≠∅，求实数m的取值范围．
18．设函数f（x）=sin（ωx+φ）（ω＞0，-π＜φ＜0）的最小正周期是π，其图象的一条对称轴是直线x=$\frac{π}{8}$，又锐角三角形ABC中，满足f（C）=-$\frac{{\sqrt{2}}}{2}$
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若tanA-$\frac{1}{sin2A}$=tanB，求角A．
8．函数f（x）=sin（x+$\frac{π}{2}$）图象的一个对称中心为（　　）
A．（$\frac{π}{2}$，0）B．（0，1）C．（0，0）D．（-$\frac{π}{4}$，0）
15．设函数f（x）=ax-$\frac{a}{x}$-2lnx（a＞0）．
（Ⅰ）若x=2是f（x）的极值点，求f（x）的极大值；
（Ⅱ）若f（x）在定义域上是单调函数，求a的取值范围．
12．设二次函数f（x）=mx2-4x+4与g（x）=x2-4mx+4m2-4m-5，其中m∈Z且m≠0，求函数f（x）和g（x）的零点均为整数的充要条件．
13．为了应对金融危机，一公司决定从某办公室10名工作人员中裁去4人，要求A、B二人不能全部裁掉，则不同的裁员方案的种数为（　　）
A．70B．126C．182D．210

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网