题目内容
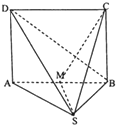 (2013•保定一模)四棱锥S-ABCD中,四边形ABCD为矩形,M为AB中点,且△SAB为等腰直角三角形,SA=SB=2,SC⊥BD,DA⊥平面SAB.
(2013•保定一模)四棱锥S-ABCD中,四边形ABCD为矩形,M为AB中点,且△SAB为等腰直角三角形,SA=SB=2,SC⊥BD,DA⊥平面SAB.(1)求证:平面SBD⊥平面SMC
(2)设四棱锥S-ABCD外接球的球心为H,求棱锥H-MSC的高.
分析:(1)要证明面面垂直,常用其判定定理来证明,即在其中一个平面内找到一条直线与另一平面垂直;
(2)空间中求距离,可用空间向量来解决,也可用等体积法来做.
(2)空间中求距离,可用空间向量来解决,也可用等体积法来做.
解答:解:(1)∵SA=SB,M为AB中点,∴SM⊥AB
又∵DA⊥平面SAB,∴DA⊥SM,∴SM⊥平面ABCD
又∵DB?平面ABCD,∴SM⊥DB
又SC⊥BD,∴DB⊥平面SMC,∴平面SBD⊥平面SMC.
(2)由(1)知DB⊥平面SMC,∴DB⊥MC
∴△ABD∽△BCM,故
=
⇒
=
⇒BC=2
设AC∩BD=N,∵AS⊥BS,DA⊥BS,∴SB⊥平面SAD
∴SB⊥SD,显然NA=NB=NC=ND=NS,所以H与N重合,即为球心.
法一:连接MH,∵SM⊥平面ABCD
∴S△HMC=S△ABC-S△AMH-S△MBC=
(2×2
-
-2
)=
,
且S△MSC=
MC×SM=
×
=
,
设棱锥H-MSC的高是h,则S△HMC×SM=S△MSC×h,
∴h=
=
=
.
法二:以点M为原点,分别以MS,MB,MH为X,Y,Z轴建立空间直角坐标系,
则M(0,0,0),B(0,
,0),C(0,
,2),H(0,0,1)
所以
=(0,-
,-1),
=(0,-
,1),|
|=
,
设棱锥H-MSC的高为h,则
•
=|
|•|
|cos<
,
>=h×|
|
∴h=
=
=
.
又∵DA⊥平面SAB,∴DA⊥SM,∴SM⊥平面ABCD
又∵DB?平面ABCD,∴SM⊥DB
又SC⊥BD,∴DB⊥平面SMC,∴平面SBD⊥平面SMC.
(2)由(1)知DB⊥平面SMC,∴DB⊥MC
∴△ABD∽△BCM,故
| AB |
| BC |
| DA |
| MB |
2
| ||
| BC |
| BC | ||
|
设AC∩BD=N,∵AS⊥BS,DA⊥BS,∴SB⊥平面SAD
∴SB⊥SD,显然NA=NB=NC=ND=NS,所以H与N重合,即为球心.
法一:连接MH,∵SM⊥平面ABCD
∴S△HMC=S△ABC-S△AMH-S△MBC=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
且S△MSC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2+4 |
| 2 |
| 3 |
设棱锥H-MSC的高是h,则S△HMC×SM=S△MSC×h,
∴h=
| S△HMC×SM |
| S△MSC |
| 1 | ||
|
| ||
| 3 |
法二:以点M为原点,分别以MS,MB,MH为X,Y,Z轴建立空间直角坐标系,
则M(0,0,0),B(0,
| 2 |
| 2 |
所以
| CH |
| 2 |
| BH |
| 2 |
| BH |
| 3 |
设棱锥H-MSC的高为h,则
| CH |
| BH |
| CH |
| BH |
| CH |
| BH |
| BH |
∴h=
| ||||
|
|
| 2-1 | ||
|
| ||
| 3 |
点评:本题考查立体几何,主要考查面面垂直,与求空间距离的问题,属于中档题.要求考生要熟练掌握此类考题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•保定一模)三棱锥V-ABC的底面ABC为正三角形,侧面VAC垂直于底面,VA=VC,已知其正视图(VAC)的面积为
(2013•保定一模)三棱锥V-ABC的底面ABC为正三角形,侧面VAC垂直于底面,VA=VC,已知其正视图(VAC)的面积为