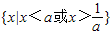题目内容
设a>1,则关于x的不等式a(x-a)•(x-
)<0的解集为( )
| 1 |
| a |
分析:先根据a>1将原不等式化成(x-a)•(x-
)<0,再利用相应的方程的根的大小情况,根据方程与不等式的联系,从而求出不等式的解.
| 1 |
| a |
解答:解:∵a>1,
∴关于x的不等式a(x-a)•(x-
)<0即:(x-a)•(x-
)<0
考察方程(x-a)•(x-
)=0的两个根a,
,
由于a>1,∴a>
,
∴不等式a(x-a)•(x-
)<0的解集为{x|
<x<a}.
故选D.
∴关于x的不等式a(x-a)•(x-
| 1 |
| a |
| 1 |
| a |
考察方程(x-a)•(x-
| 1 |
| a |
| 1 |
| a |
由于a>1,∴a>
| 1 |
| a |
∴不等式a(x-a)•(x-
| 1 |
| a |
| 1 |
| a |
故选D.
点评:本题主要考查了一元二次不等式的解法,属于基础题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
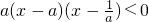 的解集为
的解集为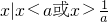
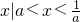
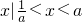
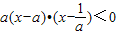 的解集为( )
的解集为( )