题目内容
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 有相同的焦点,且椭圆
有相同的焦点,且椭圆![]() 过点
过点![]() .
.
(I)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若椭圆![]() 的右顶点为
的右顶点为![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(
两点(![]() 与
与![]() 点不重合),且满足
点不重合),且满足![]() ,若点
,若点![]() 为
为![]() 中点,求直线
中点,求直线![]() 斜率的最大值.
斜率的最大值.

【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:
(Ⅰ)写出抛物线焦点坐标,得椭圆中![]() ,把点
,把点![]() 的坐标代入椭圆方程得
的坐标代入椭圆方程得![]() 与
与![]() 联立可解得
联立可解得![]() ,得椭圆方程;
,得椭圆方程;
(Ⅱ)设![]() ,设直线方程为
,设直线方程为![]() ,与椭圆方程联立消元后应用教研室可得
,与椭圆方程联立消元后应用教研室可得![]() ,
,![]() ,用
,用![]() 代
代![]() 可得F点坐标,计算中点P坐标,计算AP的斜率为
可得F点坐标,计算中点P坐标,计算AP的斜率为![]() ,分子分母同时除以
,分子分母同时除以![]() ,并换元
,并换元![]() ,得
,得![]() ,由基本不等式可得最大值.
,由基本不等式可得最大值.
试题解析:
(Ⅰ)因为抛物线![]() 的焦点为
的焦点为![]() ,抛物线与椭圆C有相同的焦点
,抛物线与椭圆C有相同的焦点
所以![]() ,又椭圆
,又椭圆![]() 过点
过点![]() ,所以
,所以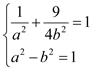 解得
解得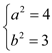 .
.
则椭圆的标准方程为![]() ;
;
(Ⅱ)设![]() ,
,![]()
直线AE的方程为![]() ,代入椭圆方程,可得
,代入椭圆方程,可得![]()
由![]() ,可得
,可得![]() ,
,![]() ,
,
由于AE⊥AF,只要将上式的![]() 换为
换为![]() ,可得
,可得![]() ,
,![]() ,
,
由P为EF的中点,得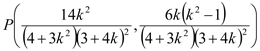
则直线AP的斜率为![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,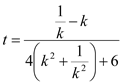 ,
,
再令![]() ,可得
,可得![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,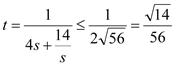 ,
,
当且仅当![]() 时,取得最大值;
时,取得最大值;
综上可得直线AP的斜率的最大值为![]() .
.

练习册系列答案
相关题目