��Ŀ����
ijͶ�ʹ�˾��2011���������a��ԪͶ�ʵ�����̼����-�ϣ�����������Ŀ��ѡ����Ŀһ�����г����У�Ͷ�ʵ�����Ŀ�ϣ�������ܻ���40%��Ҳ���ܿ���40%������������������ĸ��ʷֱ�Ϊ
 ��
�� ��
����Ŀ�������г����У�Ͷ�ʵ�����Ŀ�ϣ�������ܻ���50%��������ʧ��Ҳ���ܲ��ⲻٍ������������������ĸ��ʷֱ�Ϊ
 ��
�� ��
�� ��
����1���������ܺ��Ͷ����Ŀ�������Ի���Ϊ��ΪͶ�ʹ�˾��һ������ѡ��˵�����ɣ�
��2�����г�Ԥ�ڲ��䣬��Ͷ�ʹ�˾������ѡ�����Ŀ����Ͷ�ʣ�ÿһ�������ͱ����������Ͷ�ʣ����ʴ�Լ����һ���������ʲ�������+���𣩿��Է�һ�������ο�����lg2=0.3010��lg3=0.4771��
���𰸡���������1����һ������ֲ������⣬������ֱ�д��������Ŀ�»����ı�����1��Ԫ�ķֲ��������Ϊ��2��Ԫ���ֲ��У��ֱ�������ǵ��������Ƚ�������С����ѡ��
��2������n������ʲ����Է�һ����������ã�a×��1+20%��n=2a�������n�����ж���ݣ�
����⣺��1����������Ŀһ��Ͷ�ʣ�����Ϊ��1��Ԫ�����1�ķֲ���Ϊ

��E��1=0.4a× -0.4a×
-0.4a× =0.2a��Ԫ
=0.2a��Ԫ
������Ŀ��Ͷ�ʣ������Ϊ��2��Ԫ�����2�ķֲ���Ϊ
��E��2=0.5a× -0.36a×
-0.36a× +0×
+0× =0.18a��Ԫ��
=0.18a��Ԫ��
��E��2��E��1
��Ͷ�ʹ�˾Ӧѡ����Ŀһ
��2������n������ʲ����Է�һ����������ã�a×��1+20%��n=2a����1.2n=2��
����ͬʱȡ�����ã�n= =
= =
= ��3.8
��3.8
���Դ�Լ����4�꣬����2014������ʲ����Է�һ����
���������⿼����ɢ����������������뷽�����Ĺؼ��Ǹ�������İ�����������ǡ���ĸ���ģ�ͣ���������У����ù�ʽ���������������ֵ��Ļ�����������ȷѡ��Ӧ������ص㣬������ת��Ϊ��ѧ���⣬����𰸣��ٷ�����ʵ��������ȥ�����ʵ�����⣮
��2������n������ʲ����Է�һ����������ã�a×��1+20%��n=2a�������n�����ж���ݣ�
����⣺��1����������Ŀһ��Ͷ�ʣ�����Ϊ��1��Ԫ�����1�ķֲ���Ϊ

��E��1=0.4a×
 -0.4a×
-0.4a× =0.2a��Ԫ
=0.2a��Ԫ������Ŀ��Ͷ�ʣ������Ϊ��2��Ԫ�����2�ķֲ���Ϊ

��E��2=0.5a×
 -0.36a×
-0.36a× +0×
+0× =0.18a��Ԫ��
=0.18a��Ԫ����E��2��E��1
��Ͷ�ʹ�˾Ӧѡ����Ŀһ
��2������n������ʲ����Է�һ����������ã�a×��1+20%��n=2a����1.2n=2��
����ͬʱȡ�����ã�n=
 =
= =
= ��3.8
��3.8���Դ�Լ����4�꣬����2014������ʲ����Է�һ����
���������⿼����ɢ����������������뷽�����Ĺؼ��Ǹ�������İ�����������ǡ���ĸ���ģ�ͣ���������У����ù�ʽ���������������ֵ��Ļ�����������ȷѡ��Ӧ������ص㣬������ת��Ϊ��ѧ���⣬����𰸣��ٷ�����ʵ��������ȥ�����ʵ�����⣮

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
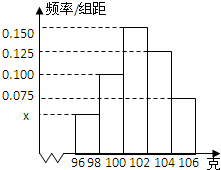 ij��˾�Թ���A��һ����Ʒ�����˳�����⣮��ͼ�Ǹ��ݳ�������IJ�Ʒ���أ���λ���ˣ����ݻ��Ƶ�Ƶ�ʷֲ�ֱ��ͼ�����в�Ʒ���صķ�Χ��[96��106]���������ݷ���Ϊ[96��98����[98��100����[100��102����[102��104����[104��106]��
ij��˾�Թ���A��һ����Ʒ�����˳�����⣮��ͼ�Ǹ��ݳ�������IJ�Ʒ���أ���λ���ˣ����ݻ��Ƶ�Ƶ�ʷֲ�ֱ��ͼ�����в�Ʒ���صķ�Χ��[96��106]���������ݷ���Ϊ[96��98����[98��100����[100��102����[102��104����[104��106]�� ��
�� ��
�� ��
�� ��
�� ��
��