Question

当实数m分别取什么值时，复数z=(1+i)m²+(5-2i)m+6-15i是（1）实数??（2）虚数?（3）纯虚数?（4）对应点在第三象限?

Answer 1

解:z=（1+i）m²+（5-2i）m+6-15i=（m²+5m+6）+（m²-2m-15）i,?

因为m∈R，所以z的实部为m²+5m+6;虚部为m²-2m-15.?

（1）z为实数，即m²-2m-15=0,?

解得m=5或m=-3.?

故当m=5或-3时，z为实数.?

（2）z为虚数,则m²-2m-15≠0,即m≠5且m≠-3.故当m≠5且m≠-3,m∈R时，z为虚数.?

（3）z为纯虚数，则实部为0，虚部不为零.?

即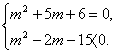解得M=-2.?

故当m=-2时，z为纯虚数.?

（4）实部与虚部均小于0时，复数z的对应点在第三象限,

即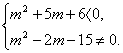解得-3＜M＜-2.?

故当-3＜m＜-2时，复数z对应的点在第三象限.