ЬтФПФкШн
(Рэ)вбжЊЧњЯпC:f(x)=x2,CЩЯЕуAЁЂAnЕФКсзјБъЗжБ№ЮЊ1КЭan(nЁЪN*),Чвa1=5,xn+1=af(xn-1)+1(aЃО0,aЁй(1)ЪдХаЖЯ:Ъ§Са{loga(xn-1)+1}ЪЧЪВУДЪ§Са;
(2)ЕБDn![]() Dn+1ЖдвЛЧаnЁЪN*КуГЩСЂЪБ,ЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇ;
Dn+1ЖдвЛЧаnЁЪN*КуГЩСЂЪБ,ЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇ;
(3)МЧЪ§Са{an}ЕФЧАnЯюКЭЮЊSn,ЕБa=![]() ЪБ,ЪдБШНЯSnгыn+7ЕФДѓаЁ,ВЂЫЕУїФуЕФНсТл.
ЪБ,ЪдБШНЯSnгыn+7ЕФДѓаЁ,ВЂЫЕУїФуЕФНсТл.
(ЮФ)вбжЊf(x)=ax3+bx2+cx+d(aЁй0)ЪЧЖЈвхдкRЩЯЕФКЏЪ§,ЦфЭМЯѓНЛxжсгкAЁЂBЁЂCШ§Еу.ШєЕуBЕФзјБъЮЊ(2,0),Чвf(x)дкЃл-1,0ЃнКЭЃл4,5ЃнЩЯгаЯрЭЌЕФЕЅЕїад,дкЃл0,2ЃнКЭЃл4,5ЃнЩЯгаЯрЗДЕФЕЅЕїад.
(1)ЧѓcЕФжЕ.
(2)дкКЏЪ§f(x)ЕФЭМЯѓЩЯЪЧЗёДцдквЛЕуM(x0,y0),ЪЙЕУf(x)дкЕуMДІЕФЧаЯпаБТЪЮЊ3b?ШєДцдк,ЧѓГіЕуMЕФзјБъ;ШєВЛДцдк,ЧыЫЕУїРэгЩ.
(3)Чѓ|AC|ЕФШЁжЕЗЖЮЇ.
Д№АИЃК(Рэ)Нт:(1)ЪЧЕШБШЪ§Са.2ЗжгЩЕуPnДІЕФЧаЯпгыжБЯпAAnЦНааПЩжЊ,xn=![]() .
.
гЩxn+1=af(xn-1)+1(aЃО0,aЁй![]() ,aЁй1)ПЩжЊxn+1-1=a(xn-1)2,дђloga(xn+1-1)=2loga(xn-1)+1.Щшbn=loga(xn-1),дђbn+1+1=2(bn+1).гжb1=loga(x1-1)=loga2,вђДЫЪ§Са{bn+1}ЪЧвдb1+1ЮЊЪзЯю,2ЮЊЙЋБШЕФЕШБШЪ§Са,МД{loga(xn-1)+1}ЪЧЕШБШЪ§Са.
,aЁй1)ПЩжЊxn+1-1=a(xn-1)2,дђloga(xn+1-1)=2loga(xn-1)+1.Щшbn=loga(xn-1),дђbn+1+1=2(bn+1).гжb1=loga(x1-1)=loga2,вђДЫЪ§Са{bn+1}ЪЧвдb1+1ЮЊЪзЯю,2ЮЊЙЋБШЕФЕШБШЪ§Са,МД{loga(xn-1)+1}ЪЧЕШБШЪ§Са.
дђbn+1=(loga2+1)ЁЄ2n-1,МДbn=(loga2+1)ЁЄ2n-1-1=loga![]() ,Ёрxn=1+
,Ёрxn=1+![]()
![]() .
.
(2)гЩЬѕМўxn=![]() ПЩжЊan=1+
ПЩжЊan=1+![]()
![]() .гЩDn
.гЩDn![]() Dn+1жЊanЃОan+1,МД
Dn+1жЊanЃОan+1,МД![]()
![]() Ѓл1-
Ѓл1-![]() ЃнЃО0,дђЃл1-
ЃнЃО0,дђЃл1-![]() ЃнЃО0,МД0ЃМaЃМ
ЃнЃО0,МД0ЃМaЃМ![]() .
.
(3)Ъ§Са{an}ЕФЧАnЯюКЭSn,ЕБa=![]() ЪБ,an=1+
ЪБ,an=1+![]()
![]() =1+8
=1+8![]() .
.
Sn=n+8Ѓл![]() +(
+(![]() )2+(
)2+(![]() )4+Ё+
)4+Ё+![]() Ѓн.ПЩвджЄУї:ЕБnЁн4,га2n-1ЃОn+1;ЁрЕБnЁм3ЪБ,SnЁмn+8Ѓл
Ѓн.ПЩвджЄУї:ЕБnЁн4,га2n-1ЃОn+1;ЁрЕБnЁм3ЪБ,SnЁмn+8Ѓл![]() +(
+(![]() )2+(
)2+(![]() )4Ѓн=n+
)4Ѓн=n+![]() ЃМn+7;
ЃМn+7;
ЕБnЁн4ЪБ,SnЃМn+8Ѓл![]() +(
+(![]() )2+(
)2+(![]() )4+(
)4+(![]() )5+(
)5+(![]() )6+Ё+(
)6+Ё+(![]() )n+1Ѓн=n+7-(
)n+1Ѓн=n+7-(![]() )n-2ЃМn+7,дђSnЃМn+7.
)n-2ЃМn+7,дђSnЃМn+7.
(ЮФ)НтЃК(1)Ёпf(x)дкЃл-1,0ЃнКЭЃл0,2ЃнЩЯгаЯрЗДЕФЕЅЕїад,Ёрx=0ЪЧf(x)ЕФвЛИіМЋжЕЕу.ЙЪfЁф(0)=0,2ЗжМД3ax2+2bx+c=0гавЛИіНтx=0,дђc=0.
(2)Ёпf(x)НЛxжсгкЕуB(2,0),Ёр8a+4b+d=0,МДd=-4(b+2a).СюfЁф(x)=0ЕУ3ax2+2bx=0,x1=0,x2=![]() .
.
Ёпf(x)дкЃл0,2ЃнКЭЃл4,5ЃнЩЯгаЯрЗДЕФЕЅЕїад,Ёр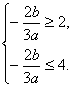 Ёр-6Ём
Ёр-6Ём![]() Ём-3.
Ём-3.
МйЩшДцдкЕуM(x0,y0),ЪЙЕУf(x)дкЕуMДІЕФЧаЯпаБТЪЮЊ3b,дђfЁф(x0)=3b,МД3ax02+2bx0-3b=0.
ЁпІЄ=(2b)2-4ЁС3aЁС(-3b)=4b2+36ab=4ab(![]() +9),Жј-6Ём
+9),Жј-6Ём![]() Ём-3,ЁрІЄЃМ0.ЙЪВЛДцдкЕуM(x0,y0),ЪЙЕУf(x)дкЕуMДІЕФЧаЯпаБТЪЮЊ3b.
Ём-3,ЁрІЄЃМ0.ЙЪВЛДцдкЕуM(x0,y0),ЪЙЕУf(x)дкЕуMДІЕФЧаЯпаБТЪЮЊ3b.
(3)ЩшA(ІС,0),C(ІТ,0),вРЬтвтПЩСюf(x)=a(x-ІС)(x-2)(x-ІТ)=aЃлx3-(2+ІС+ІТ)x2+(2ІС+2ІТ+ІСІТ)x-2ІСІТЃн,
дђ![]() МД
МД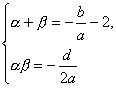 Ёр|AC|=|ІС-ІТ|=
Ёр|AC|=|ІС-ІТ|=![]()
=![]() =
=![]() .ЁВЁпd=-4(b+2a)ЁГЁп-6Ём
.ЁВЁпd=-4(b+2a)ЁГЁп-6Ём![]() Ём-3,ЁрЕБ
Ём-3,ЁрЕБ![]() =-6ЪБ,|AC|max=
=-6ЪБ,|AC|max=![]() ;ЕБ
;ЕБ![]() =-3ЪБ,|AC|min=3.ЙЪ3Ём|AC|Ём
=-3ЪБ,|AC|min=3.ЙЪ3Ём|AC|Ём![]() .
.

 ССЕуМЄЛюОЋБрЬсгХ100ЗжДѓЪдОэЯЕСаД№АИ
ССЕуМЄЛюОЋБрЬсгХ100ЗжДѓЪдОэЯЕСаД№АИ
| |||||||||||||||||||