题目内容
给出下列四个命题,其中错误的命题有( )个.
(1)函数f(x)=ex-2的零点落在区间(0,1)内;
(2)函数y=sin2x+cos2x在x∈[0,
]上的单调递增区间是[0,
];
(3)设A、B、C∈(0,
),且sinA-sinC=sinB,cosA+cosC=cosB,则B-A 等于-
;
(4)方程sin2x+2sinx+a=0有解,则a的取值范围是[-3,1].
(1)函数f(x)=ex-2的零点落在区间(0,1)内;
(2)函数y=sin2x+cos2x在x∈[0,
| π |
| 2 |
| π |
| 8 |
(3)设A、B、C∈(0,
| π |
| 2 |
| π |
| 3 |
(4)方程sin2x+2sinx+a=0有解,则a的取值范围是[-3,1].
分析:A中由根的存在性定理只需判断f(0)f(1)的符号;B中函数y=sin2x+cos2x=
sin(2x+
),再利用三角函数的图象进行判断;C中因为SinA-SinC=SinB,所以sinc=sina-sinb,那么(sinC)2=(sinA-sinB)2=(sinA)2-2sinA•sinB+(sinB)2,因为CosA+CosC=CoSB,所以cosC=cosB-cosA. 同理(cosC)2=(cosB)2-2cosA•cosB+(cosA)2,由此利用三角函知识进行求解;D中,方程sin2x+2sinx+a=0在x∈R上有解,可以转化为a=-sin2x-2sinx,x∈R.故令t=sinx∈[-1,1],则方程转化为a=-t2-2t,t∈[-1,1],借助二次函数的性质进行求解.
| 2 |
| π |
| 4 |
解答:解:A中f(0)f(1)=-1(e-2)<0,
由根的存在性定理函数函数f(x)=ex-2的零点落在区间(0,1)内;
B中函数y=sin2x+cos2x=
sin(2x+
),它在x∈[0,
]上的单调递增区间是[0,
];
C中因为SinA-SinC=SinB,所以sinc=sina-sinb,
那么(sinC)2=(sinA-sinB)2=(sinA)2-2sinA•sinB+(sinB)2,
∵CosA+CosC=CoSB,
∴cosC=cosB-cosA.
同理(cosC)2=(cosB)2-2cosA•cosB+(cosA)2,
所以相加得1=1-2(cosA•cosB+sinA•sinB)+1,
公式cos(A-B)=cosA•cosB+sinA•sinB,
∴所以相加得1=1-2cos(A-B)+1,
2cos(A-B)=1
所以cos(A-B)=
.
因为A,B,C∈(0,
),
所以0<A-B<
,
因此A-B=
,
则B-A=-
.
D中,方程sin2x+2sinx+a=0在x∈R上有解,可以转化为a=-sin2x-2sinx,x∈R
故令t=sinx∈[-1,1],则方程转化为
a=-t2-2t,t∈[-1,1],
此二次函数的对称轴为t=-1,故 a=a=-t2-2t在[-1,1]上是减函数,
∴-1≤t≤3,即a的取值范围是[-1,1].
综上所述,D不正确.
故选B.
由根的存在性定理函数函数f(x)=ex-2的零点落在区间(0,1)内;
B中函数y=sin2x+cos2x=
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
C中因为SinA-SinC=SinB,所以sinc=sina-sinb,
那么(sinC)2=(sinA-sinB)2=(sinA)2-2sinA•sinB+(sinB)2,
∵CosA+CosC=CoSB,
∴cosC=cosB-cosA.
同理(cosC)2=(cosB)2-2cosA•cosB+(cosA)2,
所以相加得1=1-2(cosA•cosB+sinA•sinB)+1,
公式cos(A-B)=cosA•cosB+sinA•sinB,
∴所以相加得1=1-2cos(A-B)+1,
2cos(A-B)=1
所以cos(A-B)=
| 1 |
| 2 |
因为A,B,C∈(0,
| π |
| 2 |
所以0<A-B<
| π |
| 2 |
因此A-B=
| π |
| 3 |
则B-A=-
| π |
| 3 |
D中,方程sin2x+2sinx+a=0在x∈R上有解,可以转化为a=-sin2x-2sinx,x∈R
故令t=sinx∈[-1,1],则方程转化为
a=-t2-2t,t∈[-1,1],
此二次函数的对称轴为t=-1,故 a=a=-t2-2t在[-1,1]上是减函数,
∴-1≤t≤3,即a的取值范围是[-1,1].
综上所述,D不正确.
故选B.
点评:本题考查函数的零点问题、三角函数的性质和运用、角的求法和参数取值范围的考查,考查知识点较多,但难度不大.

练习册系列答案
相关题目


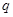 是等比数列
是等比数列 的公比,则“数列
的公比,则“数列 ”的既不充分也不必要条件;
”的既不充分也不必要条件; 上的函数
上的函数 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意 必有
必有 ;
; 满足
满足 ,则
,则 的一个正周期为
的一个正周期为 ;
; 与
与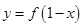 图像关于
图像关于 对称.
对称.