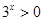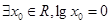题目内容
已知命题p:“?x∈[1,2],x2-a≥0”,命题q:“?x∈R”,x2+2ax+2-a=0,若命题“p∧q”是真命题,则实数a的取值范围是( )
| A.a≤-2或a=1 | B.a≤-2或1≤a≤2 |
| C.a≥1 | D.-2≤a≤1 |
A
试题分析:命题p为真命题时,要使?x∈[1,2],x2-a≥0,只需
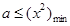 ,因为x∈[1,2]所以
,因为x∈[1,2]所以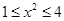 ,所以
,所以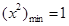 ,所以
,所以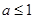 ①;命题q为真命题时,“?x∈R”,x2+2ax+2-a=0,即x2+2ax+2-a=0有实数根,所以
①;命题q为真命题时,“?x∈R”,x2+2ax+2-a=0,即x2+2ax+2-a=0有实数根,所以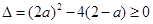 ,解得
,解得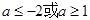 ②。因为“p∧q”是真命题,所以p,q均为真命题。①②取交集得a≤-2或a=1 ,故A正确。
②。因为“p∧q”是真命题,所以p,q均为真命题。①②取交集得a≤-2或a=1 ,故A正确。
练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 ,则
,则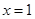 ”的逆否命题为“若
”的逆否命题为“若 ,则
,则 ”;
”; 中,
中, 增加1个单位时,
增加1个单位时, 一定增加2个单位;
一定增加2个单位; 为假命题,则
为假命题,则 均为假命题;
均为假命题;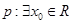 ,使得
,使得 ,则
,则 ,均有
,均有 ;
;

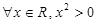
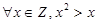
 ,使得
,使得 ”的否定为( )
”的否定为( ) ,都有
,都有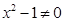
 ,都有
,都有 ” 的否定为( )
” 的否定为( )  ,使得
,使得 ;
;  ;
; ;
; 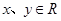 ,命题
,命题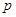 为
为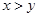 ,命题
,命题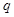 为
为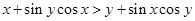 .则命题
.则命题 ”的逆否命题为:“若
”的逆否命题为:“若 ”
” ”的充分不必要条件
”的充分不必要条件 为假命题,则p、q均为假命题
为假命题,则p、q均为假命题
 ,则
,则
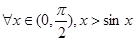
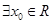 ,
,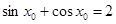
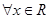 ,
,