题目内容
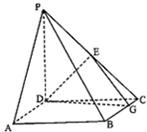 如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,
如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,| CG |
| 1 |
| 3 |
| CB |
(I)求证:PC⊥BC;
(II)求三棱锥C-DEG的体积;
(III)AD边上是否存在一点M,使得PA∥平面MEG.若存在,求AM的长;否则,说明理由.
分析:(I)由PD⊥BC,BC⊥CD,推出BC⊥平面PCD,从而证明 PC⊥BC.
(II)由GC是三棱锥G-DEC的高,三棱锥C-DEG的体积和三棱锥G-DEC的体积相等,
通过求三棱锥G-DEC的体积得到三棱锥C-DEG的体积.
(III)连接AC,取AC中点O,连接EO、GO,延长GO交AD于点M,则PA∥平面MEG,由三角形相似可得 AM=CG=
.
(II)由GC是三棱锥G-DEC的高,三棱锥C-DEG的体积和三棱锥G-DEC的体积相等,
通过求三棱锥G-DEC的体积得到三棱锥C-DEG的体积.
(III)连接AC,取AC中点O,连接EO、GO,延长GO交AD于点M,则PA∥平面MEG,由三角形相似可得 AM=CG=
| 2 |
| 3 |
解答: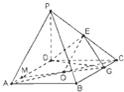 解:(I)证明:∵PD⊥平面ABCD,∴PD⊥BC,(1分)
解:(I)证明:∵PD⊥平面ABCD,∴PD⊥BC,(1分)
又∵ABCD是正方形,∴BC⊥CD,(2分)∵PDICE=D,
∴BC⊥平面PCD,又∵PC?面PBC,∴PC⊥BC.(4分)
(II)解:∵BC⊥平面PCD,
∴GC是三棱锥G-DEC的高.(5分)
∵E是PC的中点,∴S△EDC=
S△EDC=
S△PDC=
•(
•2•2)=1.(6分)
∴VC-DEG=VG-DEC=
GC•S△DEC=
•
•1=
.(8分)
(III)连接AC,取AC中点O,连接EO、GO,延长GO交AD于点M,则PA∥平面MEG.(9分)
下面证明之:
∵E为PC的中点,O是AC的中点,∴EO∥平面PA,(10分)
又∵EO?平面MEG,PA?平面MEG,∴PA∥平面MEG,(11分)
在正方形ABCD中,∵O是AC中点,∴△OCG≌△OAM,
∴AM=CG=
,∴所求AM的长为
. (12分)
 解:(I)证明:∵PD⊥平面ABCD,∴PD⊥BC,(1分)
解:(I)证明:∵PD⊥平面ABCD,∴PD⊥BC,(1分)又∵ABCD是正方形,∴BC⊥CD,(2分)∵PDICE=D,
∴BC⊥平面PCD,又∵PC?面PBC,∴PC⊥BC.(4分)
(II)解:∵BC⊥平面PCD,
∴GC是三棱锥G-DEC的高.(5分)
∵E是PC的中点,∴S△EDC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴VC-DEG=VG-DEC=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
(III)连接AC,取AC中点O,连接EO、GO,延长GO交AD于点M,则PA∥平面MEG.(9分)
下面证明之:
∵E为PC的中点,O是AC的中点,∴EO∥平面PA,(10分)
又∵EO?平面MEG,PA?平面MEG,∴PA∥平面MEG,(11分)
在正方形ABCD中,∵O是AC中点,∴△OCG≌△OAM,
∴AM=CG=
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题主要考查线面平行与垂直关系、多面体体积计算等基础知识,考查空间想象能、逻辑思维能力、运算求解能力和探究能力、考查数形结合思想、化归与转化思想.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=